3 Assume Dt D1 Dn And D 1 C1 C2 Cn Are Chegg

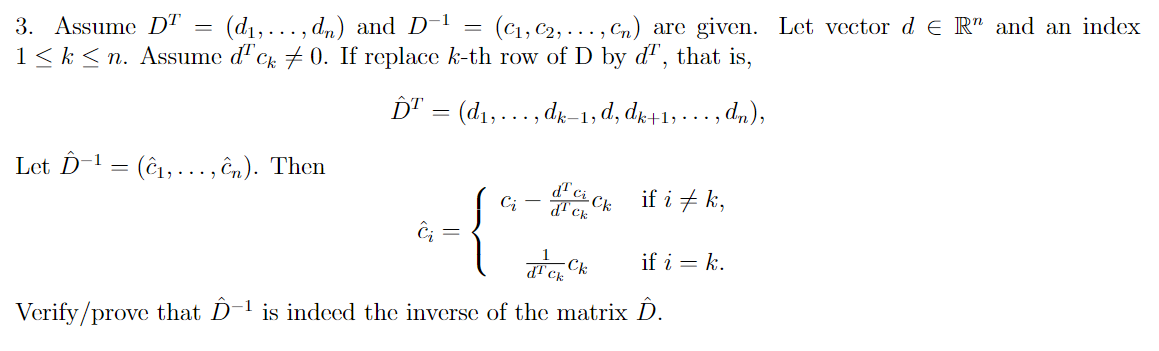
3 Assume Dt D1 Dn And D 1 C1 C2 Cn Chegg Assume d t = (d 1 , …, d n ) and d − 1 = (c 1 , c 2 , …, c n ) are given. let vector d ∈ r n and an index 1 ≤ k ≤ n . assume d t c k = 0 . 3.54 log concavity of gaussian cumulative distribution function. the cumulative distribu tion function of a gaussian random variable, f(x) = 1 √ 2π z x −∞ e−t2 2 dt, is log concave. this follows from the general result that the convolution of two log concave functions is log concave. in this problem we guide you through a simple.

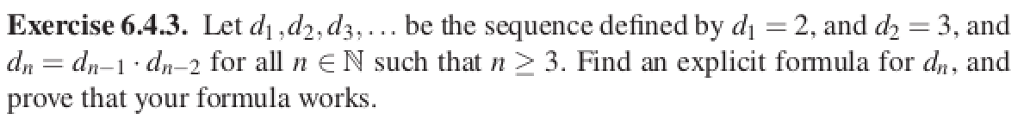
Solved Let D 1 D 2 D 3 Be The Sequence Defined By D 1 Chegg Solution for = 3. assume dt (d₁, , dn) and d 1 (c₁, c₂, , cn) are given. let vector de rn and an index 1 ≤ k ≤n. assume d ck ‡0. if replace k th row of d by…. 1(lnt) and y 2(lnt) form a fundamental set of solutions of eq. (ii). solution make the substitution x= lntin the ode. then ex = t ! e2x = t2; and the ode becomes e2x d 2y dt2 ex dy dt y= 0: the aim now is to find what the derivatives are in terms of this new variable by using the chain rule. dy dt = dy dx dx dt = dy dx 1 t = dy dx 1 ex = e. Let an = 1 (3n − 1) for n = 1, 2, 3, . write out the the first three terms of the following sequences. (a) bn = an 1 b1 = b2 = b3 = (b) cn = an 3 c1 = c2 = c3 = (c) dn = an2 d1 = d2 = d3 = (d) en = 2an − an 1 e1 = e2 = e3 = your solution’s ready to go!. Since s is linearly independent, c1 d1 = 0 and cn dn = 0 because its only the trivial solution. therefore c1=d1 and cn=dn, and is therefore unique. see an expert written answer!.

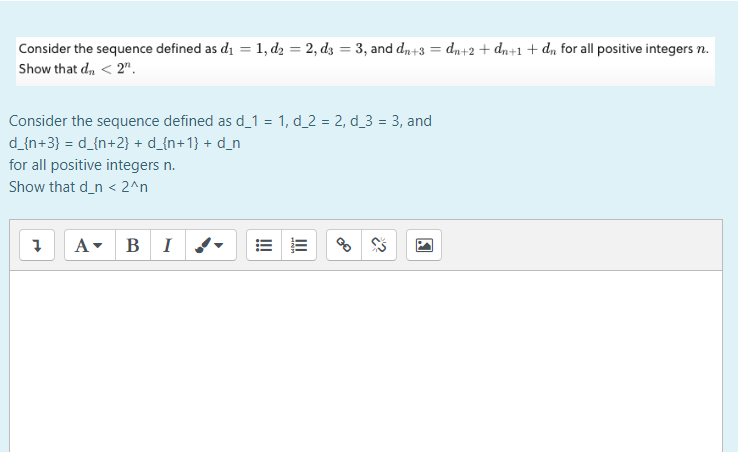
Solved Consider The Sequence Defined As Di 1 D2 2 D3 Chegg Let an = 1 (3n − 1) for n = 1, 2, 3, . write out the the first three terms of the following sequences. (a) bn = an 1 b1 = b2 = b3 = (b) cn = an 3 c1 = c2 = c3 = (c) dn = an2 d1 = d2 = d3 = (d) en = 2an − an 1 e1 = e2 = e3 = your solution’s ready to go!. Since s is linearly independent, c1 d1 = 0 and cn dn = 0 because its only the trivial solution. therefore c1=d1 and cn=dn, and is therefore unique. see an expert written answer!. Video answer: the inverse is equal to 1 divided by 2, minus minus 1 and t equal to in the formula of inverse, if we substitute an equal 3 e, equal minus 1 equals minus 4 and t equal to in the formula of inverse. Solution manual for data mining: concepts and techniques, 2nd edition. includes solutions to exercises. university level. A. use the approximate derivative dn dt ≃ (n(t ∆t)−n(t)) ∆t and find an approximate equations in terms of n (m 1), n m and n (m−1). Answer to 3. assume dt=(d1,…,dn) and d−1=(c1,c2,…,cn) are.