Basic Properties Of Logarithms Examples

Properties Of Logarithms Pdf In mathematics, properties of logarithms functions are used to solve logarithm problems. we have learned many properties in basic maths such as commutative, associative and distributive, which are applicable for algebra. Logarithm rules are the properties or the identities of the logarithm that are used to simplify complex logarithmic expressions and solve logarithmic equations involving variables. they are derived from the exponent rules, as they are just the opposite of writing an exponent. here is the list of all the logarithmic identities.

Lesson 34 Properties Of Logarithms Pdf We can use these properties to expand logarithms involving products, quotients, and powers using sums, differences and coefficients. a logarithmic expression is completely expanded when the properties of the logarithm can no further be applied. The properties of log include product, quotient, and power rules of logarithms. they are very helpful in expanding or compressing logarithms. let us learn the logarithmic properties along with their derivations and examples. Learn the fundamental properties of logarithms, including product, quotient, and power rules. this comprehensive guide explains how to use logarithmic properties to simplify calculations, solve equations, and apply them in real world scenarios. Properties of logarithm – explanation & examples. before getting into the properties of logarithms, let’s briefly discuss the relationship between logarithms and exponents. the logarithm of a number is defined as t the power or index to which a given base must be raised to obtain the number.
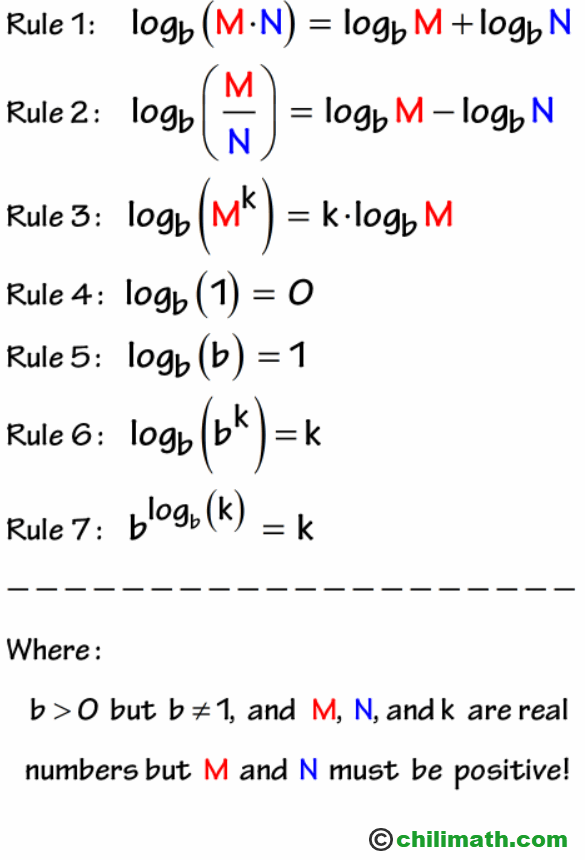
Basic Properties Of Logarithms Examples Learn the fundamental properties of logarithms, including product, quotient, and power rules. this comprehensive guide explains how to use logarithmic properties to simplify calculations, solve equations, and apply them in real world scenarios. Properties of logarithm – explanation & examples. before getting into the properties of logarithms, let’s briefly discuss the relationship between logarithms and exponents. the logarithm of a number is defined as t the power or index to which a given base must be raised to obtain the number. Exclude from the solution set any proposed solution that produces the log of a negative number or the log of 0. the怍 = log −1 does not work since it produces of a negative怍 = 3 number. therefore, the solution is: 5. solve by using the division ln( 怍 2) − ln(4 怍 3) = ln property: 1 怍 ln 4xx 3 xx 2 xx 2 = = ln xx. Logarithms can have decimals. all of our examples have used whole number logarithms (like 2 or 3), but logarithms can have decimal values like 2.5, or 6.081, etc. Understanding properties of logarithms. properties of logarithms refer to the set of algebraic rules that simplify the manipulation of log expressions. these include the product rule, quotient rule, and power rule. In this tutorial we will cover the properties of logarithms and use them to perform expansions and contractions. log = log as you can see, this rule allows us to pull the exponent down from of the log. lets’ apply the power rule in some examples as seen below.

Properties Of Logarithms Example 4 Video Calculus Ck 12 Foundation Exclude from the solution set any proposed solution that produces the log of a negative number or the log of 0. the怍 = log −1 does not work since it produces of a negative怍 = 3 number. therefore, the solution is: 5. solve by using the division ln( 怍 2) − ln(4 怍 3) = ln property: 1 怍 ln 4xx 3 xx 2 xx 2 = = ln xx. Logarithms can have decimals. all of our examples have used whole number logarithms (like 2 or 3), but logarithms can have decimal values like 2.5, or 6.081, etc. Understanding properties of logarithms. properties of logarithms refer to the set of algebraic rules that simplify the manipulation of log expressions. these include the product rule, quotient rule, and power rule. In this tutorial we will cover the properties of logarithms and use them to perform expansions and contractions. log = log as you can see, this rule allows us to pull the exponent down from of the log. lets’ apply the power rule in some examples as seen below.

Basic Properties Of Logarithms Examples Understanding properties of logarithms. properties of logarithms refer to the set of algebraic rules that simplify the manipulation of log expressions. these include the product rule, quotient rule, and power rule. In this tutorial we will cover the properties of logarithms and use them to perform expansions and contractions. log = log as you can see, this rule allows us to pull the exponent down from of the log. lets’ apply the power rule in some examples as seen below.
Comments are closed.