Chap 04 Real Analysis Mathematics Differentiation Derivative Of A Function Theorem And

Chap 04 Real Analysis Mathematics Differentiation Derivative Of A Function Theorem And The document discusses differentiation and derivatives. it defines the derivative of a function, gives examples of functions that are and aren't differentiable, and presents theorems about differentiation including the chain rule. We thus associate a function f ¢ with the function f , where domain of f ¢ is the set of points at which the above limit exists. the function f ¢ is so defined is called the derivative of f . if f ¢ is defined at point x, we say that f is differentiable at x. function j ( x ) = . let f ( x ) = xn ; n 3 0 (n is integer), x Î ¡ .

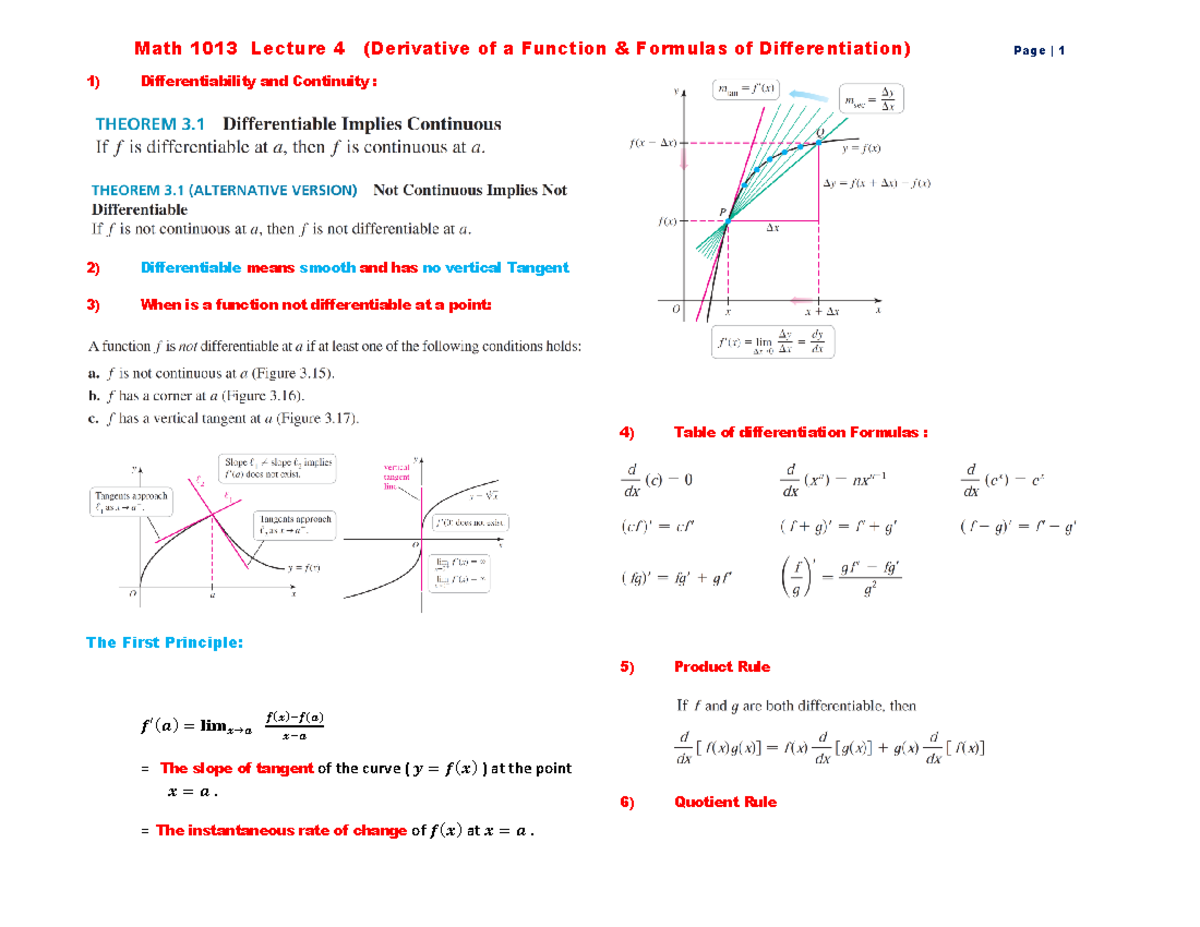
Math 1012 Lecture 4 Derivative Of A Function Formulas Of Differentiation Math 1013 Lecture Chap 04 real analysis(mathematics) '' differentiation (derivative of a function) (theorem and its proof). Taylor's theorem is a higher order version of the mean value theorem and it has abundant applications in numerical analysis. taylor's theorem involves taylor polynomials which you are familiar with from calculus. The min max theorem for continuous functions on a closed and bounded interval [a,b], the bisection method and bolzano’s intermediate value theorem. lecture 17: uniform continuity and the definition of the derivative (pdf). Differentiation 3 32 mathematics and statistics z m dω= z ∂m ω mathematics 3a03 real analysis i instructor: david earn lecture 2 differentiation wednesday 8 january 2025 instructor: david earn mathematics 3a03 real analysis i.

Solved Practice Problems 4 Derivation And Function Chegg The min max theorem for continuous functions on a closed and bounded interval [a,b], the bisection method and bolzano’s intermediate value theorem. lecture 17: uniform continuity and the definition of the derivative (pdf). Differentiation 3 32 mathematics and statistics z m dω= z ∂m ω mathematics 3a03 real analysis i instructor: david earn lecture 2 differentiation wednesday 8 january 2025 instructor: david earn mathematics 3a03 real analysis i. Compactness and completeness in metric spaces in real analysis 1.3. sequence and series 1.3.1. convergence of sequences 1.3.2. infinite series 1.3.3. uniform convergence 1.3.4. power series 1.4. differentiation 1.4.1. mean value theorems 1.4.2. taylor series 1.4.3. functions of several variables 1.4.4. partial derivatives 1.5. integration 1.5.1. Our job in real analysis is to understand how to formally describe closeness and the process of getting \closer and closer" (limits). this course starts with very abstract concepts and gets more concrete as the semester goes on. Derivative of a scalar field is the rate of change of the scalar field in a particular direction given by a vector. let p is a point in the domain of f (x; y) and vectors v1, v2, v3, and v4 represent possible directions in which we might want to know the rate of change of f (x; y). The rule of differentiation of real valued functions are valid in case of vector valued function but the situation changes in the case of mean value theorem. v example.

2171 4 Class 4 Theorem For The Geometric View Of Differential Equations Geometric Class 4 Compactness and completeness in metric spaces in real analysis 1.3. sequence and series 1.3.1. convergence of sequences 1.3.2. infinite series 1.3.3. uniform convergence 1.3.4. power series 1.4. differentiation 1.4.1. mean value theorems 1.4.2. taylor series 1.4.3. functions of several variables 1.4.4. partial derivatives 1.5. integration 1.5.1. Our job in real analysis is to understand how to formally describe closeness and the process of getting \closer and closer" (limits). this course starts with very abstract concepts and gets more concrete as the semester goes on. Derivative of a scalar field is the rate of change of the scalar field in a particular direction given by a vector. let p is a point in the domain of f (x; y) and vectors v1, v2, v3, and v4 represent possible directions in which we might want to know the rate of change of f (x; y). The rule of differentiation of real valued functions are valid in case of vector valued function but the situation changes in the case of mean value theorem. v example.