Derivatives Of Velocity And Acceleration Pdf Derivative Velocity

Derivatives Of Velocity And Acceleration Pdf Derivative Velocity Scipy.interpolate's many interpolating splines are capable of providing derivatives. so, using a linear spline ( k=1 ), the derivative of the spline (using the derivative() method) should be equivalent to a forward difference. Valueerror: the number of derivatives at boundaries does not match: expected 2, got 0 0 while trying to use cubic interpolation in pandas on a 2d matrix. mat = pd.read csv("m.csv") mat = mat.interpolate(method='cubic') csv to reproduce can be downloaded here.

The Derivatives Pdf Velocity Acceleration You need to check for gl oes standard derivatives and gl fragment precision high in the gles2 implementation of this fragment shader. to that end, you might consider the accuracy hint for derivatives: gl fragment shader derivative hint oes (gles2, if the extension is supported) gl fragment shader derivative hint (gles3). Don’t expect speedup from pipeline derivatives. vulkan usage recommendations, samsung. pipeline derivatives let applications express "child" pipelines as incremental state changes from a similar "parent"; on some architectures, this can reduce the cost of switching between similar states. I have determined derivatives through 2 separate methods, applying a high dof cubic smooth spline and via first and second differences (lightly smoothed) and bootstrapping to approximate errors with both producing comparable results. i note that the "gam.fit3" function facilitates determining upto 2nd order derivatives but is not called directly. One of the things i'd like to do is to take partial derivatives of the expressions. so if f(x,y) = x^2 y^2 then the partial of f with respect to x would be 2x, the partial with respect to y would be 2y. i wrote a dinky function using a finite differences method but i'm running into lots of problems with floating point precision.

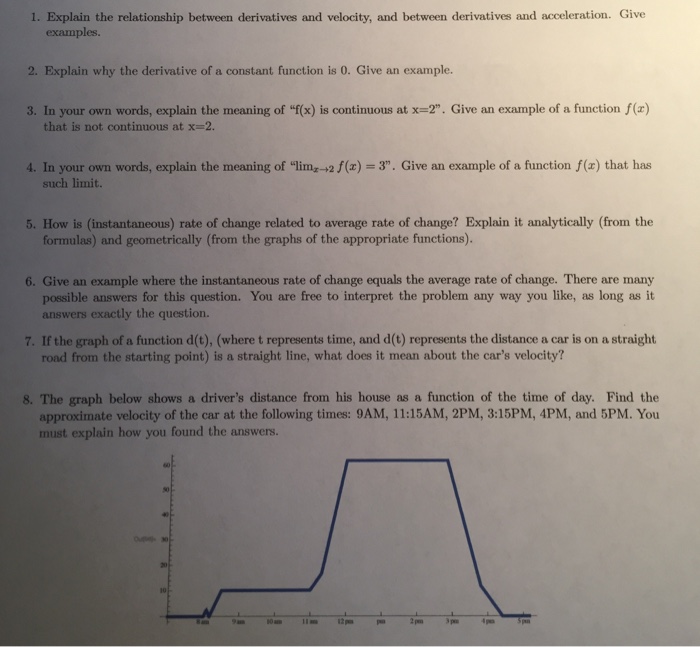
Solved 1 Explain The Relationship Between Derivatives And Chegg I have determined derivatives through 2 separate methods, applying a high dof cubic smooth spline and via first and second differences (lightly smoothed) and bootstrapping to approximate errors with both producing comparable results. i note that the "gam.fit3" function facilitates determining upto 2nd order derivatives but is not called directly. One of the things i'd like to do is to take partial derivatives of the expressions. so if f(x,y) = x^2 y^2 then the partial of f with respect to x would be 2x, the partial with respect to y would be 2y. i wrote a dinky function using a finite differences method but i'm running into lots of problems with floating point precision. Numpy.diff(x) computes the difference between adjacent elements in x. just like in the answer by @tsm. as a result you get an array which is 1 element shorter than the original one. Eigen::matrixxd derivatives(2, 1); derivatives.setzero(); derivatives zero for this example. since these are parametric splines, you have to provide derivatives for both x and y, for each of the two points you have chosen, so the correct size is: eigen::matrixxd derivatives(2, 2); derivatives.setzero(); derivatives zero for this example. I'm interested in computing partial derivatives in python. i've seen functions which compute derivatives for single variable functions, but not others. it would be great to find something that did the following. f(x,y,z) = 4xy xsin(z) x^3 z^8y part deriv(function = f, variable = x) output = 4y sin(z) 3x^2. Pinns involve computing derivatives of model outputs with respect to its inputs. these derivatives are then used to calculate pde residuals which could be heat, burger, navier stokes equation etc. therefore, one needs to compute higher order partial derivatives. i tried to use torch.autograd.grad to compute those partial derivatives. here is.

Derivatives In Engineering Velocity And Acceleration In Free Fall Docx Velocity And Numpy.diff(x) computes the difference between adjacent elements in x. just like in the answer by @tsm. as a result you get an array which is 1 element shorter than the original one. Eigen::matrixxd derivatives(2, 1); derivatives.setzero(); derivatives zero for this example. since these are parametric splines, you have to provide derivatives for both x and y, for each of the two points you have chosen, so the correct size is: eigen::matrixxd derivatives(2, 2); derivatives.setzero(); derivatives zero for this example. I'm interested in computing partial derivatives in python. i've seen functions which compute derivatives for single variable functions, but not others. it would be great to find something that did the following. f(x,y,z) = 4xy xsin(z) x^3 z^8y part deriv(function = f, variable = x) output = 4y sin(z) 3x^2. Pinns involve computing derivatives of model outputs with respect to its inputs. these derivatives are then used to calculate pde residuals which could be heat, burger, navier stokes equation etc. therefore, one needs to compute higher order partial derivatives. i tried to use torch.autograd.grad to compute those partial derivatives. here is.