Describing Transformation From The Given Graph Of Exponential Function

Describing Transformation From The Given Graph Of Exponential Function Transformations of exponential graphs behave similarly to those of other functions. just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function f (x)= bx f (x) = b x without loss of shape. Transformations regardless of the function behave the same. this graphic organizer describes transformations on the function f (x). the sections below will describe how specifically an exponential function behaves under these transformations.

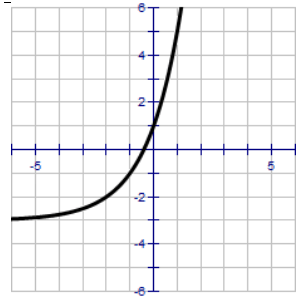
Describing Transformation From The Given Graph Of Exponential Function Transformations of exponential graphs behave similarly to those of other functions. just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function \(f(x)=b^x\) without loss of general shape. In this section, you will apply what you know about transformations of functions to graphs of exponential functions. you will perform vertical and horizontal shifts, reflections, stretches, and compressions. Compare each graph to f (x) = 2 x . write a description of each transformation and graph each function. problem 1 : solution : here the horizontal asymptote is y = 3. y = 2 x h ( 3) (1) the exponential curve is passing through the (1, 5). 5 = 21 h ( 3) 8 = 21 h. 23 = 21 h. 1 h = 3. h = 2. Consider the exponential function y 2x . for each of the transformed functions, state the parameter and describe the transformation. graph the base function and the transformed function on the same grid. describe any changes to the domain, range, intercepts, and equation of the horizontal asymptote.

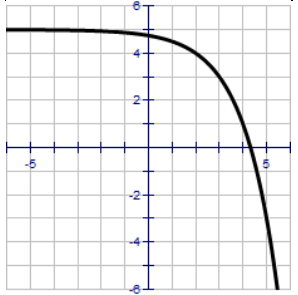
Describing Transformation From The Given Graph Of Exponential Function Compare each graph to f (x) = 2 x . write a description of each transformation and graph each function. problem 1 : solution : here the horizontal asymptote is y = 3. y = 2 x h ( 3) (1) the exponential curve is passing through the (1, 5). 5 = 21 h ( 3) 8 = 21 h. 23 = 21 h. 1 h = 3. h = 2. Consider the exponential function y 2x . for each of the transformed functions, state the parameter and describe the transformation. graph the base function and the transformed function on the same grid. describe any changes to the domain, range, intercepts, and equation of the horizontal asymptote. Transformations of exponential graphs behave similarly to those of other functions. just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function f (x) = b x f (x) = bx without loss of shape. Transformations of exponential graphs behave similarly to those of other functions. In this article, we explore these transformations in depth. transformations allow us to modify the graph of an exponential function so that it better fits empirical data or theoretical models. Graph exponential functions shifted horizontally or vertically and write the associated equation. transformations of exponential graphs behave similarly to those of other functions.

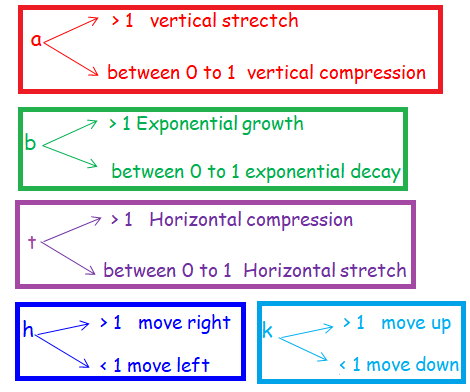
Describing Transformation From The Given Graph Of Exponential Function Transformations of exponential graphs behave similarly to those of other functions. just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function f (x) = b x f (x) = bx without loss of shape. Transformations of exponential graphs behave similarly to those of other functions. In this article, we explore these transformations in depth. transformations allow us to modify the graph of an exponential function so that it better fits empirical data or theoretical models. Graph exponential functions shifted horizontally or vertically and write the associated equation. transformations of exponential graphs behave similarly to those of other functions.

Exponential Transformations Pdf Exponential Function Function Mathematics In this article, we explore these transformations in depth. transformations allow us to modify the graph of an exponential function so that it better fits empirical data or theoretical models. Graph exponential functions shifted horizontally or vertically and write the associated equation. transformations of exponential graphs behave similarly to those of other functions.