Discrete Math Ii 10 5 2 Hamilton Paths And Circuits
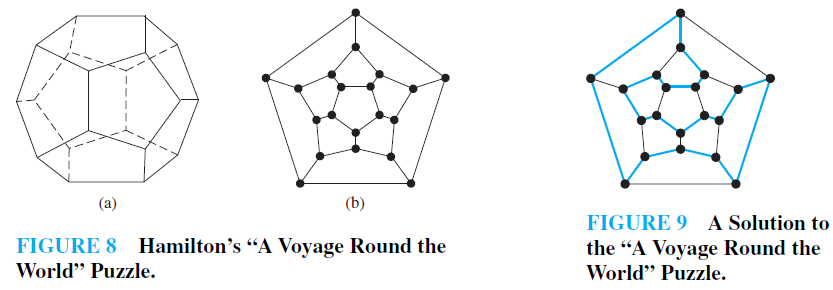
Hamilton Paths And Circuits We finish up section 10.5 by examining if it is possible to visit every vertex in a graph, rather than every edge in a graph. unfortunately, there is no algorithm and there is little guidance. 09:00 13:00: problem solving with hamilton paths and circuits the chapter titled 'problem solving with hamilton paths and circuits' explores the concept of hamilton paths and cycles in graph theory. it explains the difference between a hamilton cycle and a hamilton path through examples.
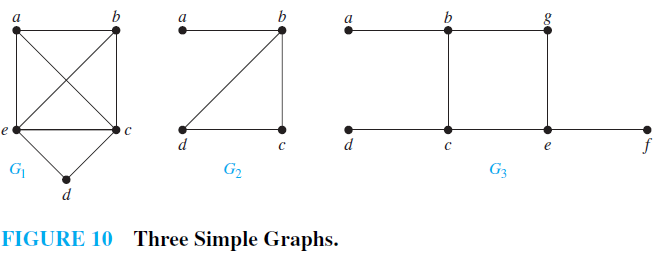
Hamilton Paths And Circuits Unlike euler paths and circuits, there are no simple necessary and sufficient criteria to determine if there are any hamiltonian paths or circuits in a graph. Not all graphs have a hamilton circuit or path. there is no way to tell just by looking at a graph if it has a hamilton circuit or path like you can with an euler circuit or path. you must do trial and error to determine this. by the way if a graph has a hamilton circuit then it has a hamilton path. just do not go back to home. Determine whether the given graph has an hamilton circuit. if it does, find such a circuit. it it does not, give an argument to show why no such circuit exists. Hamilton paths and circuits definition : a hamilton path in a graph is a path that visits each vertex exactly once. if such a path is also a circuit, it is called a hamilton circuit. •ex : 21 hamilton path hamilton circuit.
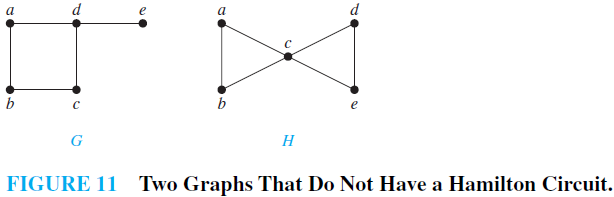
Hamilton Paths And Circuits Determine whether the given graph has an hamilton circuit. if it does, find such a circuit. it it does not, give an argument to show why no such circuit exists. Hamilton paths and circuits definition : a hamilton path in a graph is a path that visits each vertex exactly once. if such a path is also a circuit, it is called a hamilton circuit. •ex : 21 hamilton path hamilton circuit. A hamiltonian path or traceable path is a path that visits each vertex of the graph exactly once. a graph that contains a hamiltonian path is called a traceable graph.a graph is hamiltonian connected if for every pair of vertices there is a hamiltonian path between the two vertices a hamiltonian cycle, hamiltonian circuit, vertex tour or graph cycle is a cycle that visits each vertex exactly. If the degree of every vertex g is at least n=2, then g has a hamilton circuit. i ore’s theorem: if for any pair of non adjacent vertices u and v deg(u) deg(v) n then, g has a hamilton circuit. A hamiltonian path, also called a hamilton path, is a graph path between two vertices of a graph that visits each vertex exactly once. if a hamiltonian path exists whose endpoints are adjacent, then the resulting graph cycle is called a hamiltonian cycle (or hamiltonian cycle). a graph that possesses a hamiltonian path is called a traceable graph. in general, the problem of finding a. Both ore’s theorem and dirac’s theorem provide sufficient conditions for a connected simple graph to have a hamilton circuit. however, these theorems do not provide necessary conditions for the existence of a hamilton circuit.
Hamilton Paths And Circuits Discrete Mathematics Books Skedbooks A hamiltonian path or traceable path is a path that visits each vertex of the graph exactly once. a graph that contains a hamiltonian path is called a traceable graph.a graph is hamiltonian connected if for every pair of vertices there is a hamiltonian path between the two vertices a hamiltonian cycle, hamiltonian circuit, vertex tour or graph cycle is a cycle that visits each vertex exactly. If the degree of every vertex g is at least n=2, then g has a hamilton circuit. i ore’s theorem: if for any pair of non adjacent vertices u and v deg(u) deg(v) n then, g has a hamilton circuit. A hamiltonian path, also called a hamilton path, is a graph path between two vertices of a graph that visits each vertex exactly once. if a hamiltonian path exists whose endpoints are adjacent, then the resulting graph cycle is called a hamiltonian cycle (or hamiltonian cycle). a graph that possesses a hamiltonian path is called a traceable graph. in general, the problem of finding a. Both ore’s theorem and dirac’s theorem provide sufficient conditions for a connected simple graph to have a hamilton circuit. however, these theorems do not provide necessary conditions for the existence of a hamilton circuit.
Discrete Math Ii 10 5 1 Euler Paths And Circuits A hamiltonian path, also called a hamilton path, is a graph path between two vertices of a graph that visits each vertex exactly once. if a hamiltonian path exists whose endpoints are adjacent, then the resulting graph cycle is called a hamiltonian cycle (or hamiltonian cycle). a graph that possesses a hamiltonian path is called a traceable graph. in general, the problem of finding a. Both ore’s theorem and dirac’s theorem provide sufficient conditions for a connected simple graph to have a hamilton circuit. however, these theorems do not provide necessary conditions for the existence of a hamilton circuit.
Comments are closed.