Displacement Velocity Acceleration With Polynomial Derivatives Calculus

By themeroute On Aug 3, 2025

Displacement Velocity Acceleration Pdf Velocity Acceleration Integral calculus gives us a more complete formulation of kinematics. if acceleration a(t) is known, we can use integral calculus to derive expressions for velocity v(t) and position x(t). In order to find the velocity, we need to find a function of \(t\) whose derivative is constant. we are simply going to guess such a function and then we will verify that our guess has all of the desired properties.

Derivatives Of Velocity And Acceleration Pdf Derivative Velocity Speeding and slowing analysis by graph: watch?v=l8diufcopwe&list=plj ma5djyaqqaxjtmnufsvnykbo1glwym&index=5 @m. Displacement, velocity and acceleration can be expressed as functions of time. if we express these quantities as functions, they can be related by derivatives. given x(t) as displacement, v(t) as velocity and a(t) as acceleration, we can relate the functions through derivatives. Formulae for displacement, velocity and acceleration. the formula linking displacement, velocity and acceleration is s=vt 1 2 at 2, where s is displacement, v is velocity and a is acceleration. this formula works provided the acceleration is constant. Velocity and acceleration motion on a straight line one reason for introducing the derivative is the need to calculate rates of change. consider the motion of an object along a straight line.

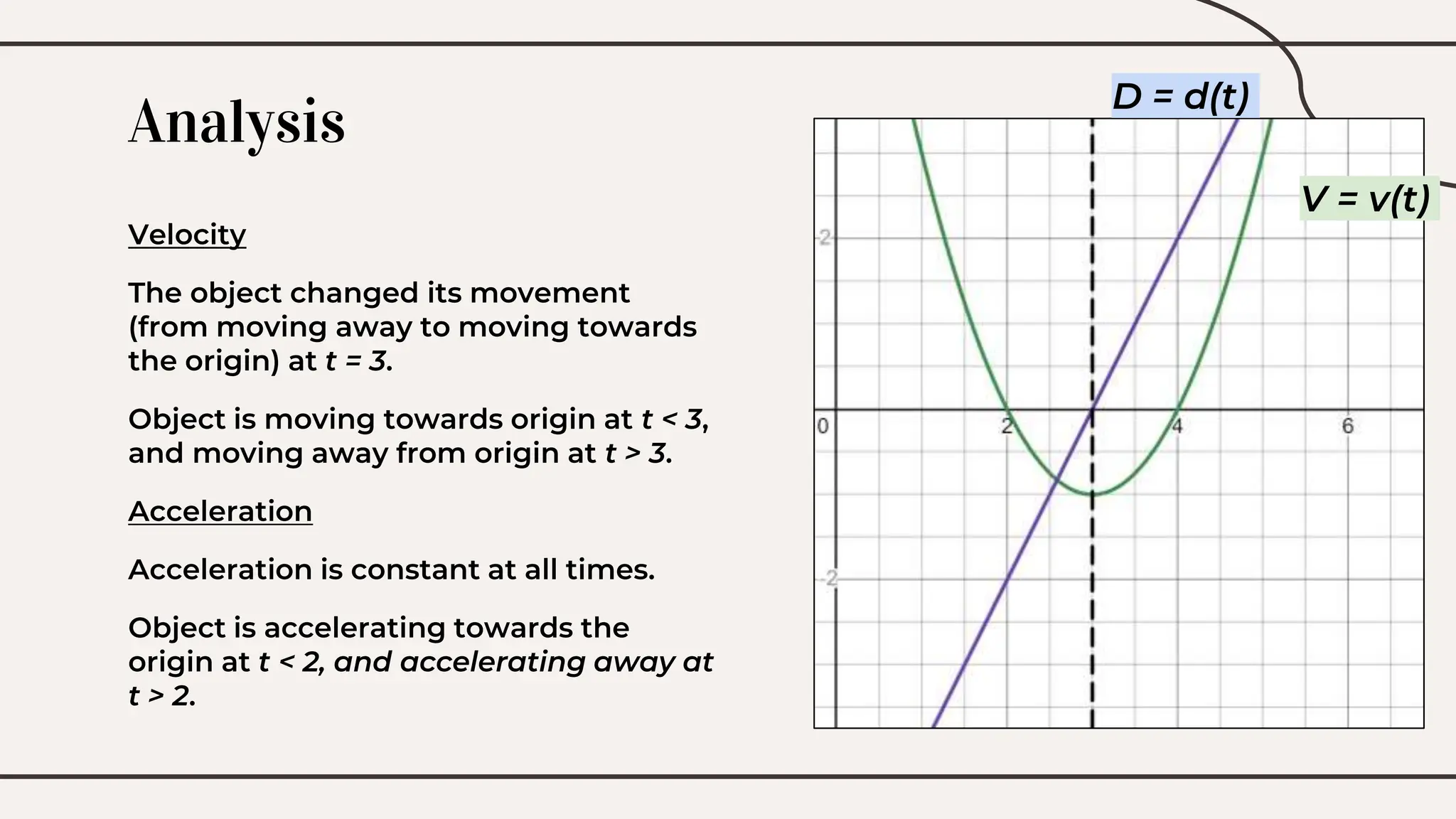
Displacement Velocity Acceleration And Second Derivatives Ppt Formulae for displacement, velocity and acceleration. the formula linking displacement, velocity and acceleration is s=vt 1 2 at 2, where s is displacement, v is velocity and a is acceleration. this formula works provided the acceleration is constant. Velocity and acceleration motion on a straight line one reason for introducing the derivative is the need to calculate rates of change. consider the motion of an object along a straight line. From the context, x x is a function of two variables, so that we use ∂ ∂ instead of d. it is just the notations. the essential question is whether the quantity k k depends on t t as well, or not. dx dt:=x˙(t) = ∂f ∂t (t, k) , d x d t:= x (t) = ∂ f ∂ t (t, k) , and similarly for the acceleration. These deriv atives can be viewed in four ways: physically, numerically, symbolically, and graphically. the ideas of velocity and acceleration are familiar in everyday experience, but now we want you to connect them with calculus. we have discussed several cases of this idea already. Now, as we usually do in calculus, we let Δt →0. the average velocity becomes the (instan taneous) velocity and the ratios in the formula above become derivatives. If acceleration a(t) is known, we can use integral calculus to derive expressions for velocity v(t) and position x(t). if acceleration is constant, the integral equations reduce to figure and figure for motion with constant acceleration.

Displacement Pdf Velocity Derivative From the context, x x is a function of two variables, so that we use ∂ ∂ instead of d. it is just the notations. the essential question is whether the quantity k k depends on t t as well, or not. dx dt:=x˙(t) = ∂f ∂t (t, k) , d x d t:= x (t) = ∂ f ∂ t (t, k) , and similarly for the acceleration. These deriv atives can be viewed in four ways: physically, numerically, symbolically, and graphically. the ideas of velocity and acceleration are familiar in everyday experience, but now we want you to connect them with calculus. we have discussed several cases of this idea already. Now, as we usually do in calculus, we let Δt →0. the average velocity becomes the (instan taneous) velocity and the ratios in the formula above become derivatives. If acceleration a(t) is known, we can use integral calculus to derive expressions for velocity v(t) and position x(t). if acceleration is constant, the integral equations reduce to figure and figure for motion with constant acceleration.

Displacement Velocity And Acceleration Introducing The Differential Calculus Coursera Now, as we usually do in calculus, we let Δt →0. the average velocity becomes the (instan taneous) velocity and the ratios in the formula above become derivatives. If acceleration a(t) is known, we can use integral calculus to derive expressions for velocity v(t) and position x(t). if acceleration is constant, the integral equations reduce to figure and figure for motion with constant acceleration.

Whether you're looking for practical how-to guides, in-depth analyses, or thought-provoking discussions, we are has got you covered. Our diverse range of topics ensures that there's something for everyone, from Displacement Velocity Acceleration With Polynomial Derivatives Calculus. We're committed to providing you with valuable information that resonates with your interests.

Displacement Velocity Acceleration with Polynomial Derivatives Calculus

Displacement Velocity Acceleration with Polynomial Derivatives Calculus

Displacement Velocity Acceleration with Polynomial Derivatives Calculus Calculus - Position Average Velocity Acceleration - Distance & Displacement - Derivatives & Limits Displacement Velocity Acceleration Derivatives Displacement, velocity and acceleration using derivatives Differential Calculus | Displacement, Velocity & Acceleration ❖ Position, Velocity, Acceleration using Derivatives ❖ Speeding Velocity Acceleration Higher Order Derivatives Application Calculus MCV4U 🚀ACCELERATION, VELOCITY and DISPLACEMENT using DERIVATIVES and INTEGRALS: Formulas and examples DIFFERENTIATION OF POLYNOMIAL FUNCTIONS || LESSON 2 || Position Velocity Acceleration Speeding Distance Derivatives Calculus MCV4U Understand Relation Between Displacement Velocity Acceleration and Higher Derivatives Applications of derivatives Displacement velocity and acceleration Velocity and Position From Acceleration By Integration - Physics and Calculus 2.3. Displacement, Velocity, Acceleration and Second Derivatives - Example1 - Part1 Differentiation - Displacement, Velocity, Acceleration Position Velocity Acceleration Higher Derivates Understand Graph and Derivatives Velocity, Acceleration and Second Derivatives DIFFERENTIATION V|KINEMATICS|DISPLACEMENT|VELOCITY| ACCELERATION|WORKED EXAMPLES Calculus Find Acceleration when velocity is 4 as a function of displacement Calculus MCV4U Physics With Calculus - Basic Introduction

Conclusion

Considering all the aspects, one can conclude that the content provides pertinent information touching on Displacement Velocity Acceleration With Polynomial Derivatives Calculus. Across the whole article, the scribe reveals extensive knowledge pertaining to the theme. Distinctly, the section on various aspects stands out as a highlight. The article expertly analyzes how these aspects relate to create a comprehensive understanding of Displacement Velocity Acceleration With Polynomial Derivatives Calculus.

Furthermore, the essay does a great job in disentangling complex concepts in an clear manner. This accessibility makes the information valuable for both beginners and experts alike. The writer further augments the discussion by embedding applicable demonstrations and practical implementations that situate the intellectual principles.

Another element that distinguishes this content is the thorough investigation of different viewpoints related to Displacement Velocity Acceleration With Polynomial Derivatives Calculus. By investigating these multiple standpoints, the piece delivers a fair understanding of the issue. The completeness with which the writer handles the matter is really remarkable and sets a high standard for analogous content in this discipline.

To conclude, this article not only informs the consumer about Displacement Velocity Acceleration With Polynomial Derivatives Calculus, but also motivates additional research into this captivating field. Should you be a beginner or an authority, you will find worthwhile information in this exhaustive post. Thank you for your attention to this article. If you have any inquiries, do not hesitate to drop a message through the discussion forum. I look forward to your questions. In addition, here is a number of connected posts that are potentially useful and enhancing to this exploration. May you find them engaging!