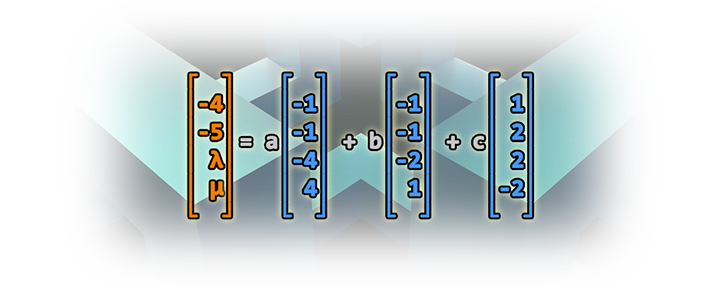
El Problema De La Semana Pertenece El Vector Al Conjunto Generador Nibcode Solutions Determinar si un vector pertenece al subespacio generado por un conjunto de vectores. la solución involucra los conceptos de rango de una matriz, transformaciones elementales y sistemas de ecuaciones. El problema de esta semana está relacionado con los sistemas generadores y las bases, dos conceptos esenciales de los espacios vectoriales que debes dominar. la solución, como es habitual en la mayoría de los problemas de álgebra lineal, utiliza los conceptos básicos de matrices y sus operaciones.
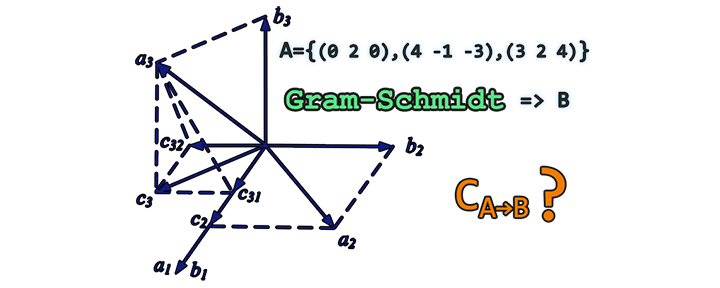
El Problema De La Semana El Proceso De Gram Schmidt Nibcode Solutions Para resolver el problema de esta semana, deberás utilizar los conceptos de vector coordenado y matriz de cambio de base, los cuales son básicos en muchos problemas prácticos. Estas tres nociones se definen en términos del producto interno de dos vectores, que también es el concepto clave para tratar las bases ortogonales, el tema del problema de esta semana. las bases ortogonales, y particularmente las bases ortonormales, son muy útiles cuando se trabaja con proyecciones sobre subespacios, entre otros problemas. Este problema de la semana tratará sobre el núcleo (el conjunto de vectores en el espacio vectorial de partida que se transforma en el vector cero) y la nulidad de una transformación lineal, y su solución solo requiere saber cómo trabajar con matrices y hacer operaciones elementales por fila. El problema de encontrar los conjuntos generadores más «pequeños» para un espacio vectorial depende de la noción de independencia lineal, que presentamos en esta sección.
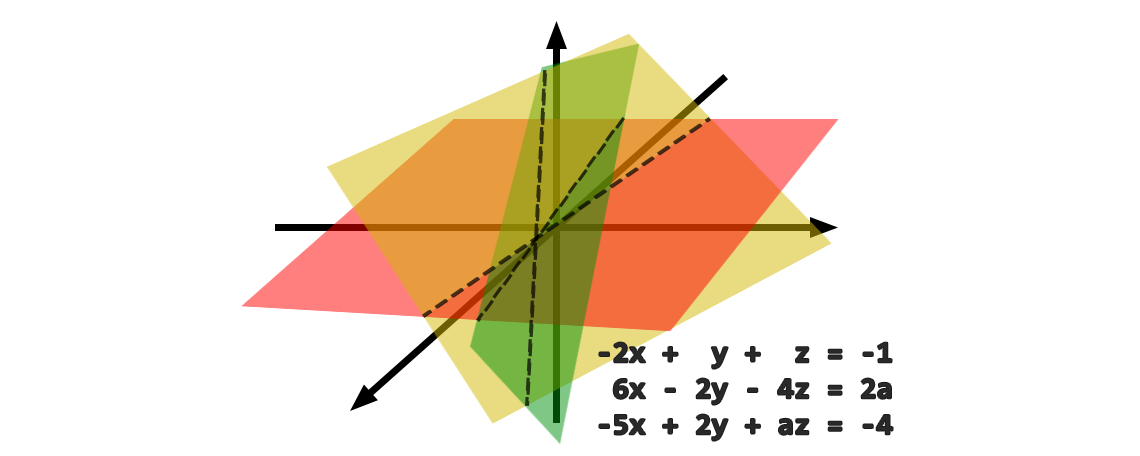
El Problema De La Semana Clasifica El Sistema De Ecuaciones Lineales Nibcode Solutions Este problema de la semana tratará sobre el núcleo (el conjunto de vectores en el espacio vectorial de partida que se transforma en el vector cero) y la nulidad de una transformación lineal, y su solución solo requiere saber cómo trabajar con matrices y hacer operaciones elementales por fila. El problema de encontrar los conjuntos generadores más «pequeños» para un espacio vectorial depende de la noción de independencia lineal, que presentamos en esta sección. Denomina conjunto generador de 𝑉 si todo vector en 𝑉 puede expresarse como una combinación lineal de vectores en 𝑆. por lo cual, se puede decir que 𝑆 genera a 𝑉. Entonces, en lugar de trabajar con p n, podemos traducir los polinomios de p n a vectores euclidianos de dimensión n 1, resolver el problema, y luego traducir la respuesta al conjunto de los polinomios, de ser necesario, utilizando la inversa de t, la cual es:. Esta semana nos dedicamos a presentar dos conceptos importantes sobre los cuales se define la noción de base para un espacio vectorial. el primero corresponde a la idea de conjunto. Propiedades: un conjunto generador puede contener más vectores de los necesarios para generar el espacio, es decir, puede ser redundante. un conjunto generador que no contiene vectores redundantes se denomina base del espacio vectorial.
Vectores Semana 1 Pdf Course Hero Denomina conjunto generador de 𝑉 si todo vector en 𝑉 puede expresarse como una combinación lineal de vectores en 𝑆. por lo cual, se puede decir que 𝑆 genera a 𝑉. Entonces, en lugar de trabajar con p n, podemos traducir los polinomios de p n a vectores euclidianos de dimensión n 1, resolver el problema, y luego traducir la respuesta al conjunto de los polinomios, de ser necesario, utilizando la inversa de t, la cual es:. Esta semana nos dedicamos a presentar dos conceptos importantes sobre los cuales se define la noción de base para un espacio vectorial. el primero corresponde a la idea de conjunto. Propiedades: un conjunto generador puede contener más vectores de los necesarios para generar el espacio, es decir, puede ser redundante. un conjunto generador que no contiene vectores redundantes se denomina base del espacio vectorial.
Comments are closed.