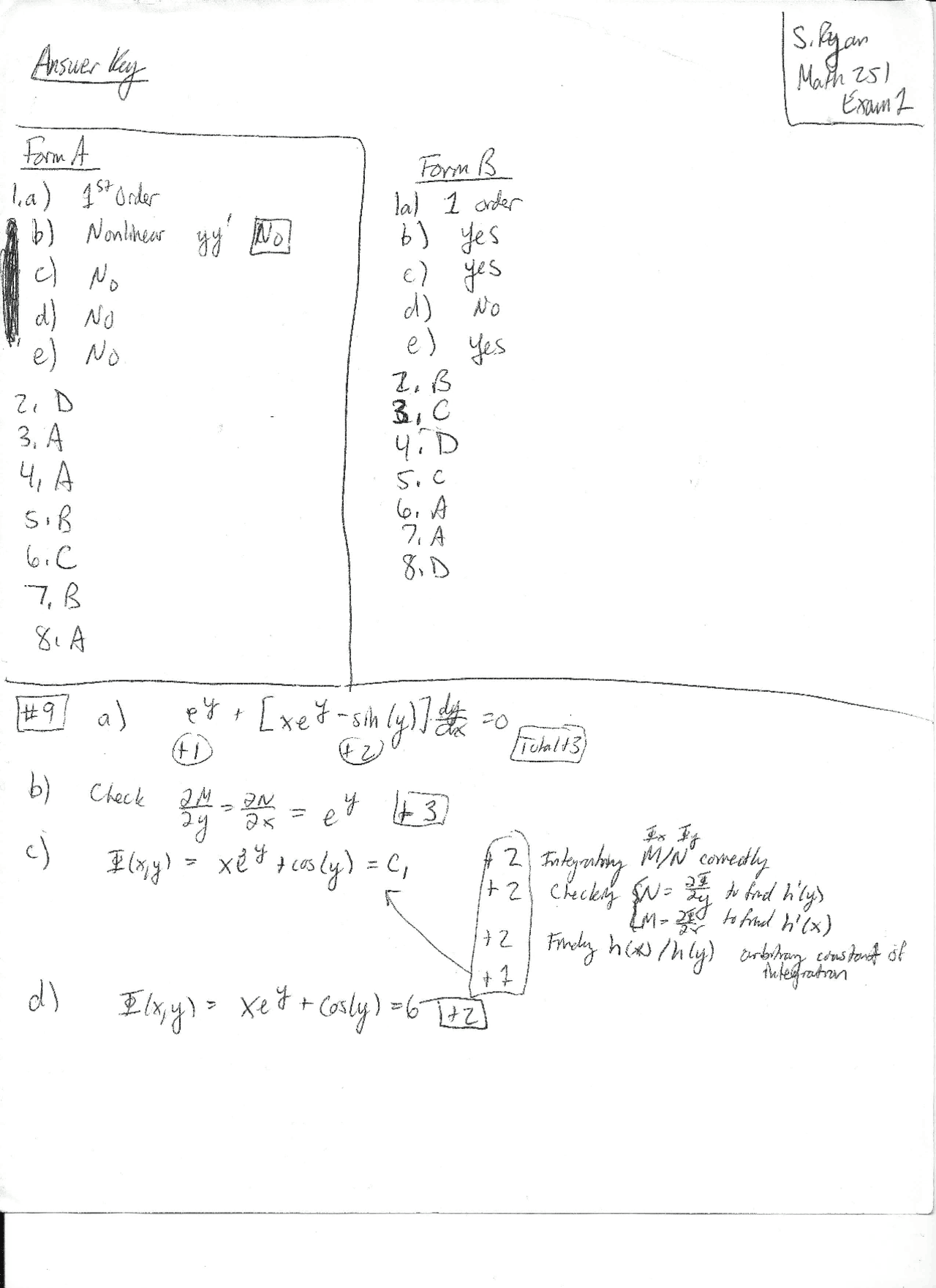
Equation Autonomous Ordinary And Partial Differential Equations Solved Exam Docsity Math 251 final examination december 14, 2011 form a name: student number: section: this exam has 18 questions for a total of 150 points. in order to obtain full credit for partial credit problems, all work must be shown. An autonomous differential equation is a differential equation where the independent variable does not appear in it. however, the measure of change of the dependent variable solely rests on the dependent variable.
Particular Solution Ordinary And Partial Differential Equations Solved Exam Examens When a differential equation involves a single independent variable, we refer to the equation as an ordinary differential equation (ode). example 1.0.2. if there are several dependent variables and a single independent variable, we might have equations such as dy dx = x2y xy2 z, dz dx = z ycos x. Instead of solving the equations they tried to show whether an equation has solutions or not, and what properties such solution may have. this is less information than obtaining the solution, but it is still valuable information. A differential equation is called autonomous if it can be written as y'(t)=f(y). autonomous differential equations are separable and can be solved by simple integration. • ordinary vs partial differential equations – a ordinary differential equation has derivatives with respect to one variable. – a partial differential equation has derivatives with respect to more than one variable.
Ordinary Differential Equations Solutions To Problem Set 1 Docsity A differential equation is called autonomous if it can be written as y'(t)=f(y). autonomous differential equations are separable and can be solved by simple integration. • ordinary vs partial differential equations – a ordinary differential equation has derivatives with respect to one variable. – a partial differential equation has derivatives with respect to more than one variable. This notes is intended for circulation to students of a course on partial differential equations. though the notes are proof read many times, it could still have some misprints. Main points of this exam paper are: autonomous, letter corresponding, erential equations, specified, order homogeneous, third order nonlinear equation, nonhomogeneous, second order, first order linear equation, equation. math 251 exam 1 july 9, 2007 answer key 1. c, e, h, d, a 2, b 3. c 4. a 5. a 6. Ordinary differential equations review “the profound study of nature is the most fertile source of mathematical discover ies.” joseph fourier (1768 1830) a.1 first order differential equations before moving on, we first define an n th order ordinary differential equation. This section provides materials for a session on first order autonomous differential equations. materials include course notes, lecture video clips, practice problems with solutions, javascript mathlets, and quizzes consisting of problem sets with solutions.
Ordinary And Partial Differential Equations Pptx This notes is intended for circulation to students of a course on partial differential equations. though the notes are proof read many times, it could still have some misprints. Main points of this exam paper are: autonomous, letter corresponding, erential equations, specified, order homogeneous, third order nonlinear equation, nonhomogeneous, second order, first order linear equation, equation. math 251 exam 1 july 9, 2007 answer key 1. c, e, h, d, a 2, b 3. c 4. a 5. a 6. Ordinary differential equations review “the profound study of nature is the most fertile source of mathematical discover ies.” joseph fourier (1768 1830) a.1 first order differential equations before moving on, we first define an n th order ordinary differential equation. This section provides materials for a session on first order autonomous differential equations. materials include course notes, lecture video clips, practice problems with solutions, javascript mathlets, and quizzes consisting of problem sets with solutions.
Comments are closed.