Exponential Population Growth Model
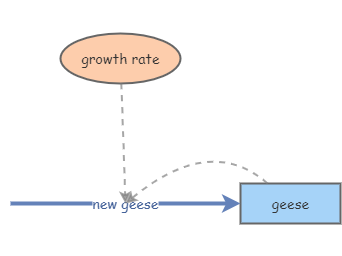
Exponential Population Growth Insight Maker What are the underlying principles of how populations change over time? two basic principles are involved, the idea of exponential growth and its ultimate control. Exponential growth happens when an initial population increases by the same percentage or factor over equal time increments or generations. this is known as relative growth and is usually expressed as percentage. for example, let’s say a population is growing by 1.6% each year.
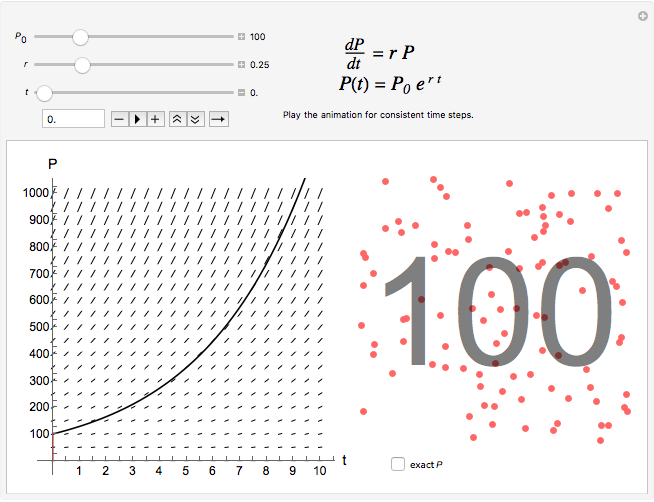
Exponential Model For Population Growth Wolfram Demonstrations Project To model the reality of limited resources, population ecologists developed the logistic growth model. in the real world, with its limited resources, exponential growth cannot continue indefinitely. This interactive simulation allows students to explore two classic mathematical models that describe how populations change over time: the exponential and logistic growth models. the exponential growth model describes how a population changes if its growth is unlimited. Exponential growth occurs when a single species is not limited by other species (no predation, parasitism, competitors), resources are not limited, and the environment is constant. these conditions called an ‘ecological vacuum’, and this does not often occur (for long) in nature. Model represents geometric population growth. later in the exercise, we will develop a continuous time model, properly called an exponential model.

Exponential Equations To Model Population Growth Krista 51 Off Exponential growth occurs when a single species is not limited by other species (no predation, parasitism, competitors), resources are not limited, and the environment is constant. these conditions called an ‘ecological vacuum’, and this does not often occur (for long) in nature. Model represents geometric population growth. later in the exercise, we will develop a continuous time model, properly called an exponential model. In fact in both cases the rate of growth r of a population (or an investment) per time period is proportional to the size of the population (or the amount of an investment). where r is the relative rate of growth of the population (expressed as a proportion of the population). One of the foundational concepts in population dynamics is the exponential growth model. this model is a simplified representation of how populations grow when resources are not limiting. Exponential growth many quantities grow or decay at a rate proportional to their size. i for example a colony of bacteria may double every hour. i if the size of the colony after thours is given by y( ), then we can express this information in mathematical language in the form of an equation: dy=dt = 2y:. The first of these models, exponential growth, describes populations that increase in numbers without any limits to their growth. the second model, logistic growth, introduces limits to reproductive growth that become more intense as the population size increases.
Resources Platform Tutorchase In fact in both cases the rate of growth r of a population (or an investment) per time period is proportional to the size of the population (or the amount of an investment). where r is the relative rate of growth of the population (expressed as a proportion of the population). One of the foundational concepts in population dynamics is the exponential growth model. this model is a simplified representation of how populations grow when resources are not limiting. Exponential growth many quantities grow or decay at a rate proportional to their size. i for example a colony of bacteria may double every hour. i if the size of the colony after thours is given by y( ), then we can express this information in mathematical language in the form of an equation: dy=dt = 2y:. The first of these models, exponential growth, describes populations that increase in numbers without any limits to their growth. the second model, logistic growth, introduces limits to reproductive growth that become more intense as the population size increases.
Comments are closed.