Graph Theory Unit 1 Pdf The tsp is more complex for non complete graphs. as we have seen, a complete graph has many hamilton circuits. in contrast, a non complete graph may have no hamilton circuit, and the problem of determining if a non complete graph has a hamilton circuit at all is a difficult one. Finding a shortest hamiltonian circuit on a weighted graph is called the traveling salesman problem (tsp) because the question can be framed like this: suppose a salesman needs to give sales pitches in four cities. he looks up the airfares between each city, and puts the costs in a graph.
Solved In Chapter Six We Learned About Hamilton Circuits Weighted Graphs And The Traveling • the traveling salesman problem is to find a minimal length hamiltonian path representing the most efficient route that a traveling salesman can use to visit the finite number of cities on his route. Listed on this page. example: willy decides to visit every australian city important enough to be. ll possible hamilton circuits. willy could so. g up the weights of its edges. willy could so. ith the smallest total weight. willy could so. x, y. elds. the . amil. on c. rcui. cn . ml . ho . ad . as . ul . bm . ku . da . m. x, y. A graph with n vertices in which every pair of distinct vertices is joined by an edge is called a complete graph on n vertices and denoted by the symbol k n . Example: use the nearest neighbor method to solve the following travelling salesman problem, for the graph shown in fig starting at vertex v 1. solution: we have to start with vertex v 1. by using the nearest neighbor method, vertex by vertex construction of the tour or hamiltonian circuit is shown in fig: the total distance of this route is 18.
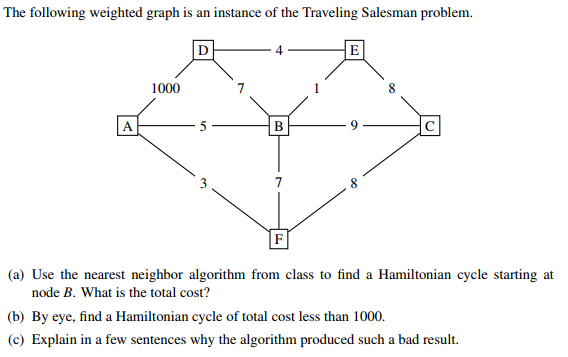
Solved The Following Weighted Graph Is An Instance Of The Chegg A graph with n vertices in which every pair of distinct vertices is joined by an edge is called a complete graph on n vertices and denoted by the symbol k n . Example: use the nearest neighbor method to solve the following travelling salesman problem, for the graph shown in fig starting at vertex v 1. solution: we have to start with vertex v 1. by using the nearest neighbor method, vertex by vertex construction of the tour or hamiltonian circuit is shown in fig: the total distance of this route is 18. Definition (traveling salesman problem) thetraveling salesman problemis to find the circuit that visits every vertex and minimizes the total weight of its edges. This section we review the de nition of eulerian cycle. in the next section, we will use this notion to give a new view of the 2 approximate algorithm of the previ ous section, and we willnote that this new perspective suggests a potentially be. Definition (traveling salesman problem) thetraveling salesman problemis to find the circuit that visits every vertex and minimizes the total weight of its edges.
Solved Problem 9 10 Points Graphs Solve The Traveling Chegg Definition (traveling salesman problem) thetraveling salesman problemis to find the circuit that visits every vertex and minimizes the total weight of its edges. This section we review the de nition of eulerian cycle. in the next section, we will use this notion to give a new view of the 2 approximate algorithm of the previ ous section, and we willnote that this new perspective suggests a potentially be. Definition (traveling salesman problem) thetraveling salesman problemis to find the circuit that visits every vertex and minimizes the total weight of its edges.
Comments are closed.