How To Solve Logarithmic Equations With Different Bases

View Question Solve Logarithmic Equations With Different Bases In this explainer, we will learn how to solve logarithmic equations involving logarithms with different bases. let’s first recall the relationship between logarithmic and exponential forms. Learn how to solve logarithmic equations with different bases using the change of base formula. also check your answer for extraneous solutions. step by step.

Solving Log Equations With Different Bases Problems Solutions There are many operations that can be performed on logarithms; however, this requires that the logarithms have the same base. solving logarithms with different bases require a change of base of the logarithms, which can be performed in a few short steps. Let’s learn how to solve the logarithmic equations in arithmetic quantities with different bases by the logarithmic properties. Learn how to rewrite any logarithm using logarithms with a different base. this is very useful for finding logarithms in the calculator!. Logarithmic equations can be difficult to solve, but there are a few different methods that can be used. one common method is to use the change of base formula, which allows you to convert a logarithm with one base to a logarithm with a different base.

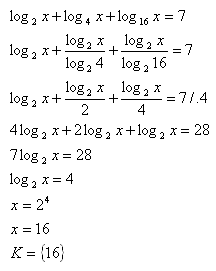
Logarithmic Equations Other Bases Examples Of Problems With Solutions Learn how to rewrite any logarithm using logarithms with a different base. this is very useful for finding logarithms in the calculator!. Logarithmic equations can be difficult to solve, but there are a few different methods that can be used. one common method is to use the change of base formula, which allows you to convert a logarithm with one base to a logarithm with a different base. How do we solve a log equation with different bases? here we will see how we can use the change of base formula for logarithm to solve log 4(x) log 2(x)=6. ?. Logarithmic equations other bases – examples of problems with solutions for secondary schools and universities. Here's a way that may be the easiest to understand, using the change of base formula in its simplest form: $$ (\log 4 7)(\log 7 5) = \frac{\log e 7}{\log e 4} \cdot \frac{\log e 5}{\log e 7} = \frac{\log e 5}{\log e 4} = \log 4 5. $$. Find the solution set of log to the base three of 𝑥 equals log to the base nine of four in the set of real numbers. so to solve this problem, what we’re going to do is actually change the base of our logarithm. and we do that using this formula here, which is that log to the base 𝑎 of 𝑏 equals log to the base 𝑥 of 𝑏 over log to the base 𝑥 of 𝑎.

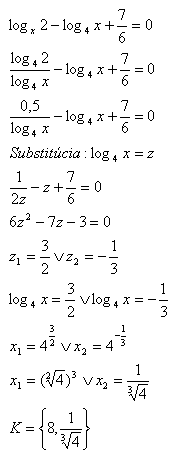
Logarithmic Equations Other Bases Examples Of Problems With Solutions How do we solve a log equation with different bases? here we will see how we can use the change of base formula for logarithm to solve log 4(x) log 2(x)=6. ?. Logarithmic equations other bases – examples of problems with solutions for secondary schools and universities. Here's a way that may be the easiest to understand, using the change of base formula in its simplest form: $$ (\log 4 7)(\log 7 5) = \frac{\log e 7}{\log e 4} \cdot \frac{\log e 5}{\log e 7} = \frac{\log e 5}{\log e 4} = \log 4 5. $$. Find the solution set of log to the base three of 𝑥 equals log to the base nine of four in the set of real numbers. so to solve this problem, what we’re going to do is actually change the base of our logarithm. and we do that using this formula here, which is that log to the base 𝑎 of 𝑏 equals log to the base 𝑥 of 𝑏 over log to the base 𝑥 of 𝑎.

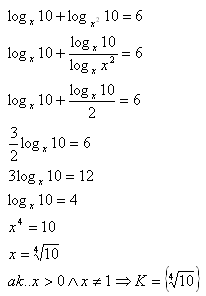
Logarithmic Equations Other Bases Examples Of Problems With Solutions Here's a way that may be the easiest to understand, using the change of base formula in its simplest form: $$ (\log 4 7)(\log 7 5) = \frac{\log e 7}{\log e 4} \cdot \frac{\log e 5}{\log e 7} = \frac{\log e 5}{\log e 4} = \log 4 5. $$. Find the solution set of log to the base three of 𝑥 equals log to the base nine of four in the set of real numbers. so to solve this problem, what we’re going to do is actually change the base of our logarithm. and we do that using this formula here, which is that log to the base 𝑎 of 𝑏 equals log to the base 𝑥 of 𝑏 over log to the base 𝑥 of 𝑎.