Templatemonster Launches Gpl Wordpress Themes Special Offer 5 Gpl Themes For 75 I know that $\\infty \\infty$ is not generally defined. however, if we have 2 equal infinities divided by each other, would it be 1? if we have an infinity divided by another half as big infinity, for. What do finite, infinite, countable, not countable, countably infinite mean? [duplicate] ask question asked 12 years, 11 months ago modified 12 years, 11 months ago.
Wordpress Plugins And Themes Available Official Gpl Elakiri Can you give me an example of infinite field of characteristic p ≠ 0 p ≠ 0? thanks. The reason being, especially in the non standard analysis case, that "infinite number" is sort of awkward and can make people think about ∞ ∞ or infinite cardinals somehow, which may be giving the wrong impression. but "transfinite number" sends, to me, a somewhat clearer message that there is a particular context in which the term takes place. The dual space of an infinite dimensional vector space is always strictly larger than the original space, so no to both questions. this was discussed on mo but i can't find the thread. 6 show that if a σ σ algebra is infinite, that it contains a countably infinite collection of disjoint subsets. an immediate consequence is that the σ σ algebra is uncountable.
Wordpress Gpl Nulled Themes Plugins Legality Risks Explained Nooblinux The dual space of an infinite dimensional vector space is always strictly larger than the original space, so no to both questions. this was discussed on mo but i can't find the thread. 6 show that if a σ σ algebra is infinite, that it contains a countably infinite collection of disjoint subsets. an immediate consequence is that the σ σ algebra is uncountable. Then prove that it holds for an index set of size n 1 n 1 and wrap it up by n → ∞ n → ∞ but i'm not convinced that's right. for example, an argument like that doesn't work for countable intersection being closed on a collection of open sets. so what's a good proof that can extend de morgan's law to an infinite collection of sets. And so on. now, it is clear that these partial sums grow without bound, so traditionally we say that the sum either doesn't exist or is infinite. so, to make the claim in your question title, you must adopt a nontraditional method of summation. there are many such methods available, but the one used in this case is zeta function regularization. If your infinite dimensional space has an inner product and is complete with respect to the induced norm then it is an infinite dimensional hilbert space. that's all it takes to make an infinite dimensional hilbert space. Why is the infinite sphere contractible? i know a proof from hatcher p. 88, but i don't understand how this is possible. i really understand the statement and the proof, but in my imagination this.
Wordpress Gpl Plugins W3templates Then prove that it holds for an index set of size n 1 n 1 and wrap it up by n → ∞ n → ∞ but i'm not convinced that's right. for example, an argument like that doesn't work for countable intersection being closed on a collection of open sets. so what's a good proof that can extend de morgan's law to an infinite collection of sets. And so on. now, it is clear that these partial sums grow without bound, so traditionally we say that the sum either doesn't exist or is infinite. so, to make the claim in your question title, you must adopt a nontraditional method of summation. there are many such methods available, but the one used in this case is zeta function regularization. If your infinite dimensional space has an inner product and is complete with respect to the induced norm then it is an infinite dimensional hilbert space. that's all it takes to make an infinite dimensional hilbert space. Why is the infinite sphere contractible? i know a proof from hatcher p. 88, but i don't understand how this is possible. i really understand the statement and the proof, but in my imagination this.
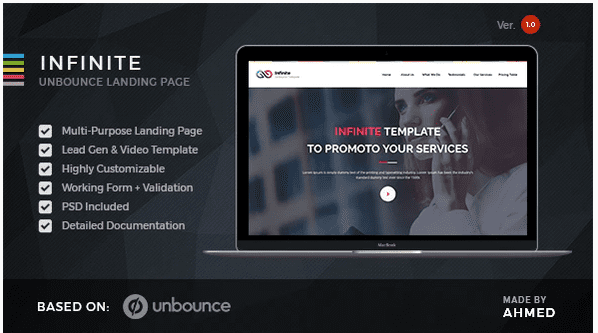
Infinite Marketing Unbounce Template Biggest Collection Of Gpl Themes Plugins Templates If your infinite dimensional space has an inner product and is complete with respect to the induced norm then it is an infinite dimensional hilbert space. that's all it takes to make an infinite dimensional hilbert space. Why is the infinite sphere contractible? i know a proof from hatcher p. 88, but i don't understand how this is possible. i really understand the statement and the proof, but in my imagination this.
Blogging Gpl Bundled Wordpress Theme Templatemonster
Comments are closed.