Logarithm Pdf

Logarithm Pdf Pdf Logarithms are defined as the solutions to exponential equations and so are practically useful in any situation where one needs to solve such equations (such as finding how long it will take for a population to double or for a bank balance to reach a given value with compound interest). historically, they were also useful because of the fact that the logarithm of a product is the sum of the. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. upvoting indicates when questions and answers are useful. what's reputation and how do i get it? instead, you can save this post to reference later.

Logarithm Formula Pdf Since the natural logarithm is indeed the natural logarithm to use in calculus, it is written as log log with no subscript. some mathematicians write it as ln ln but still understand log log written by others to mean the base e e logarithm. only among non mathematicians is that last fact unknown. what is "natural" about it can be seen here:. I would like to know how logarithms are calculated by computers. the gnu c library, for example, uses a call to the fyl2x() assembler instruction, which means that logarithms are calculated directl. So, it seems to be in summary that for all positive bases, the logarithm can't be found for negative numbers. but for some negative bases it can. am i right in this? is the requirement of a positive number within the logarithm restricted to all positive and some negative numbers?. I'm thinking of making a table of logarithms ranging from 100 999 with 5 significant digits. by pen and paper that is. i'm doing this old school. what first came to mind was to use $\\log(ab) = \\lo.

Logarithm Sheet Solution 1666958544141 Pdf Logarithm Number Theory So, it seems to be in summary that for all positive bases, the logarithm can't be found for negative numbers. but for some negative bases it can. am i right in this? is the requirement of a positive number within the logarithm restricted to all positive and some negative numbers?. I'm thinking of making a table of logarithms ranging from 100 999 with 5 significant digits. by pen and paper that is. i'm doing this old school. what first came to mind was to use $\\log(ab) = \\lo. I had "the logarithm of a number is the index to which the base is raised to equal that number" drilled into me 60 years ago. it's still helpful when i need a reminder what does what. in this context, y is the number, x is the base and y is the index. Another popular method for computing logarithms was to compute the exponential function (inverse of the desired logarithm function) of an initial guess. exponential function is a rapidly converging power series, so it is quickly computed. a solver routine then adjusts the approximation to get the desired logarithm. The point is: the complex logarithm is not a function, but what we call a multivalued function. to turn it into a proper function, we must restrict what θ θ is allowed to be, for example θ ∈ (−π, π] θ ∈ (π, π]. this is called the principal complex logarithm and is usually denoted by log log (capital l). 16 logarithm of a quantity really only makes sense if the quantity is dimensionless, and then the result is also a dimensionless number. so what you really plot is not log(y) log (y) but log(y y0) log (y y 0) where y0 y 0 is some reference quantity in the same units as y y (in this case y0 = y 0 = 1 volt). similarly for exp exp and sin sin.

Logarithms Pdf Pdf Logarithm Multiplication I had "the logarithm of a number is the index to which the base is raised to equal that number" drilled into me 60 years ago. it's still helpful when i need a reminder what does what. in this context, y is the number, x is the base and y is the index. Another popular method for computing logarithms was to compute the exponential function (inverse of the desired logarithm function) of an initial guess. exponential function is a rapidly converging power series, so it is quickly computed. a solver routine then adjusts the approximation to get the desired logarithm. The point is: the complex logarithm is not a function, but what we call a multivalued function. to turn it into a proper function, we must restrict what θ θ is allowed to be, for example θ ∈ (−π, π] θ ∈ (π, π]. this is called the principal complex logarithm and is usually denoted by log log (capital l). 16 logarithm of a quantity really only makes sense if the quantity is dimensionless, and then the result is also a dimensionless number. so what you really plot is not log(y) log (y) but log(y y0) log (y y 0) where y0 y 0 is some reference quantity in the same units as y y (in this case y0 = y 0 = 1 volt). similarly for exp exp and sin sin.

Session 7 Intro To Logarithm Reading Pdf 11 1 21 1 08 Pm Introduction To Logarithms The point is: the complex logarithm is not a function, but what we call a multivalued function. to turn it into a proper function, we must restrict what θ θ is allowed to be, for example θ ∈ (−π, π] θ ∈ (π, π]. this is called the principal complex logarithm and is usually denoted by log log (capital l). 16 logarithm of a quantity really only makes sense if the quantity is dimensionless, and then the result is also a dimensionless number. so what you really plot is not log(y) log (y) but log(y y0) log (y y 0) where y0 y 0 is some reference quantity in the same units as y y (in this case y0 = y 0 = 1 volt). similarly for exp exp and sin sin.
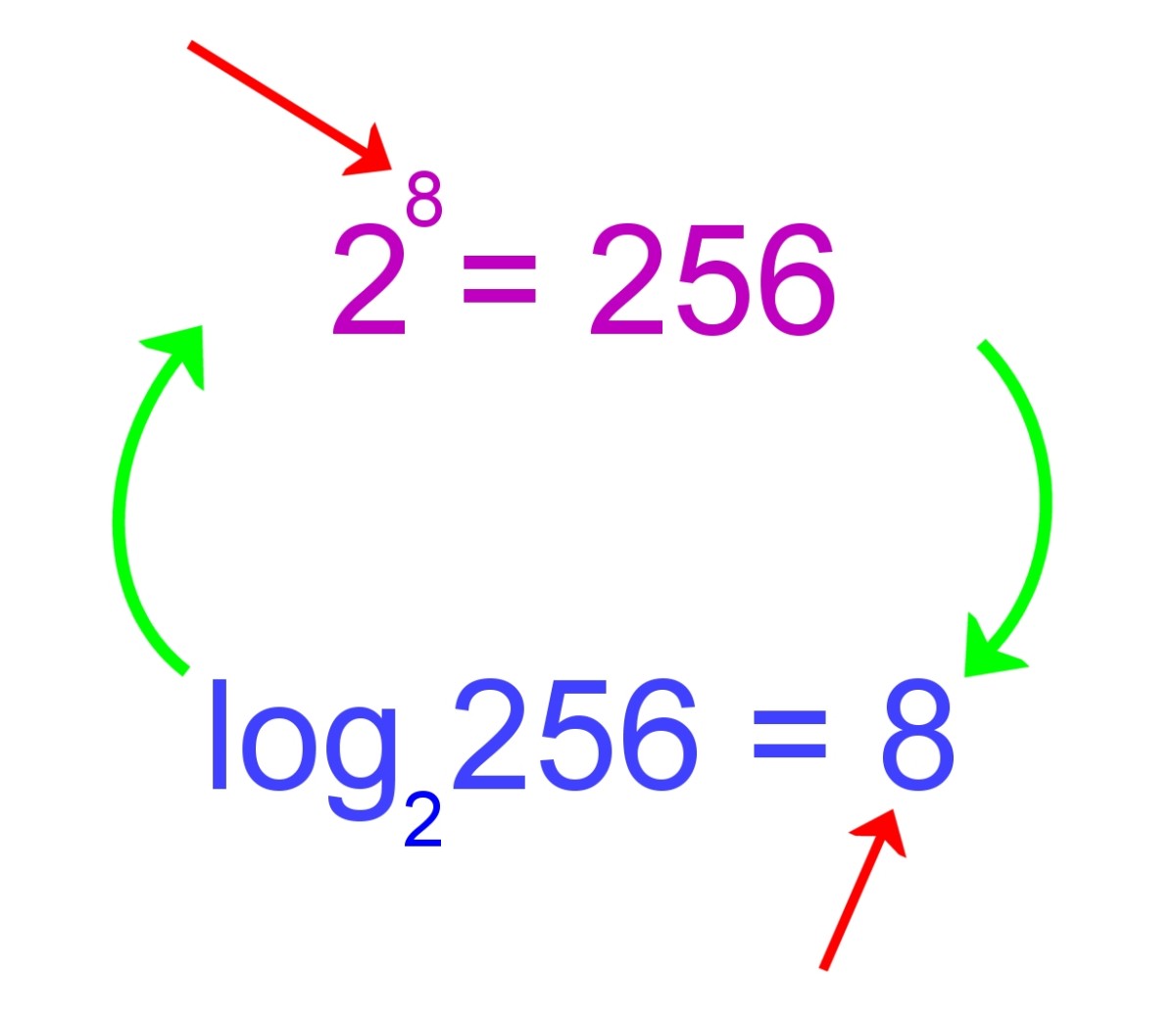
Logarithm Exercises With Answers
Comments are closed.