Logarithmic Function Differentiation How To Differentiate Logarithmic Functions Excellenceacademy

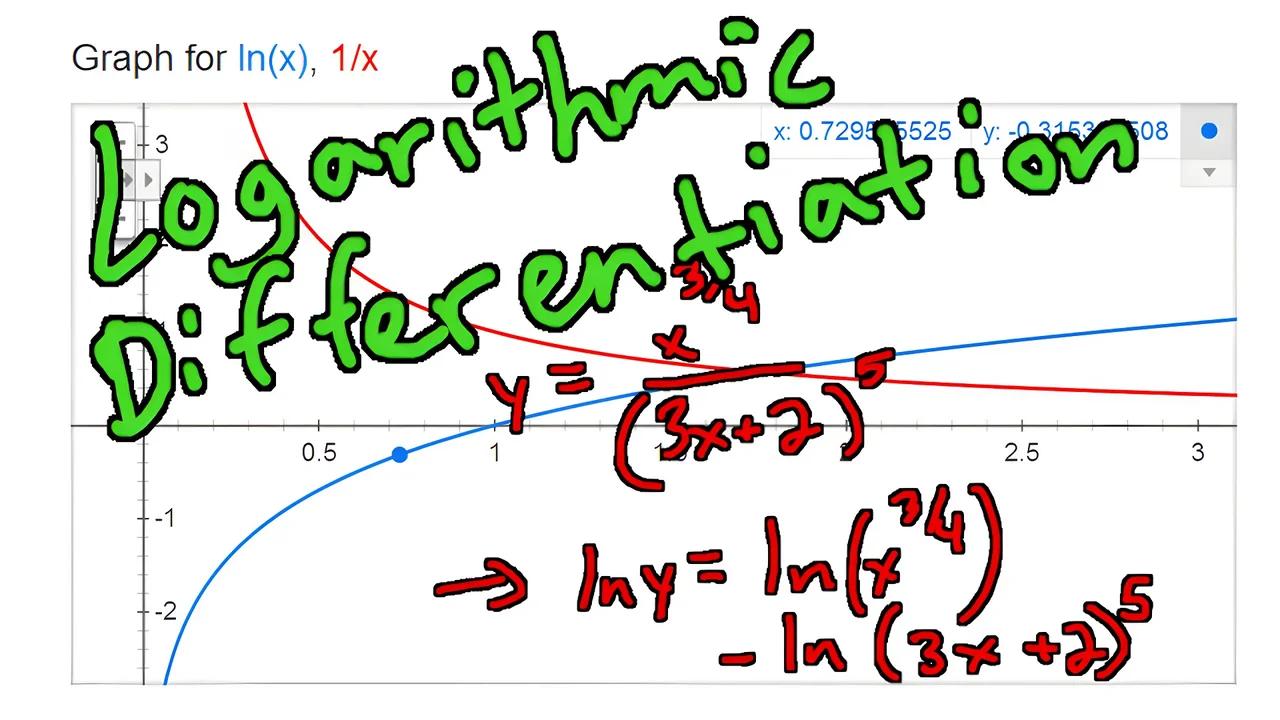
Logarithmic Differentiation Easy Way To Simplify Derivatives Taking the derivatives of some complicated functions can be simplified by using logarithms. this is called logarithmic differentiation. it’s easiest to see how this works in an example. differentiating this function could be done with a product rule and a quotient rule. however, that would be a fairly messy process. Differentiate using the formula for derivatives of logarithmic functions. don't forget the chain rule!.

Solved Differentiating Logarithmic Functions Use Chegg Finding the derivative of any logarithmic function is called logarithmic differentiation. the derivative of the natural logarithmic function (with the base ‘e’), lnx, with respect to ‘x,’ is 1 x and is given by. d d x (ln x) = (ln x) ′ = 1 x, where x > 0. Find the derivative of each function below by using logarithmic differentiation. (a) f(x) = xx f (x) = x x. (b) g(t) = (t2 1)sin(t) g (t) = (t 2 1) sin (t) (c) a(v) = (v 1) 1 ln(v 1) a (v) = (v 1) 1 ln (v 1) you don't have to use logarithmic differentiation on every piece of a function. As we learn to diferentiate all the old families of functions that we knew from algebra, trigonometry and precalculus, we run into two basic rules. the first is for polynomials. when taking the derivative of a polynomial, we use the power rule (both basic and with chain rule): 濷睮1 ך淬f\prime (x). Let's see first how to differentiate the functions that already have a product and or a quotient under the logarithm. example 1. find the derivative of y = ln. y = ln(x2 1cos(x) ). y = ln(cos(x)) −ln(x2 1). but what to do if we have products and powers but don't have the logarithm?.

Derivatives Of Logarithmic Functions Logarithmic Differentiation Lesson As we learn to diferentiate all the old families of functions that we knew from algebra, trigonometry and precalculus, we run into two basic rules. the first is for polynomials. when taking the derivative of a polynomial, we use the power rule (both basic and with chain rule): 濷睮1 ך淬f\prime (x). Let's see first how to differentiate the functions that already have a product and or a quotient under the logarithm. example 1. find the derivative of y = ln. y = ln(x2 1cos(x) ). y = ln(cos(x)) −ln(x2 1). but what to do if we have products and powers but don't have the logarithm?. These functions require a technique called logarithmic differentiation, which allows us to differentiate any function of the form h(x)= g(x)f(x) h (x) = g (x) f (x). it can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of y = x√2x 1 exsin3x y = x 2 x 1 e x sin 3 x. Logarithmic differentiation is a method to find the derivatives of some complicated functions, using logarithms. there are cases in which differentiating the logarithm of a given function is simpler as compared to differentiating the function itself. Differentiation of logarithmic functions with examples and detailed solutions. We begin by converting f(x) = loga(x) into a function with base e.

Solved Logarithmic Differentiation Differentiate Each Chegg These functions require a technique called logarithmic differentiation, which allows us to differentiate any function of the form h(x)= g(x)f(x) h (x) = g (x) f (x). it can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of y = x√2x 1 exsin3x y = x 2 x 1 e x sin 3 x. Logarithmic differentiation is a method to find the derivatives of some complicated functions, using logarithms. there are cases in which differentiating the logarithm of a given function is simpler as compared to differentiating the function itself. Differentiation of logarithmic functions with examples and detailed solutions. We begin by converting f(x) = loga(x) into a function with base e.

Differentiation Of Logarithmic Functions Logarithm Derivative Differentiation of logarithmic functions with examples and detailed solutions. We begin by converting f(x) = loga(x) into a function with base e.