Magnetic Field On Axis Of Circular Loop Physics Vidyalay

Magnetic Field On The Axis Of A Circular Current Loop Evaluate The Magnetic Field Due To A In 1820, oersted discovered that a current carrying conductor produces a magnetic field around it. biot savart law helps to calculate the magnetic field due to the current element of a thin wire. in this article, we will learn about the magnetic field on the axis of a circular loop. Before we know more about the magnetic field on the axis of a circular current loop, let us understand the basic law of magnetism. we know that there exists an equation that describes the magnetic field generated by constant current.

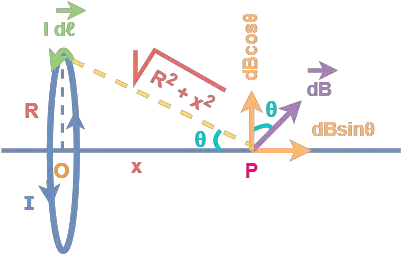
Magnetic Field On The Axis Of A Circular Current Loop Evaluate The Magnetic Field Due To A Let us take a magnetic compass and place it near a current carrying circular loop. in this case, the needle present inside the magnetic compass experiences a torque and gets deflected to align along the direction of the magnetic field. The magnetic field due to a current carrying circular loop of radius 3 cm at a point on the axis at a distance of 4 cm from the centre is 54 µt. what will be its value at the centre of the loop? a. 75 µt b. 150 µt c. 125 µt d. 250 µt. It can be resolved into two components, one is vertical component of magnitude $db\: sin\phi$ along the axis of the loop and the other is horizontal component of magnitude $db\: cos\phi$ at right angles to the axis. 🔴 magnetic field at the axis of a circular current carrying loop | class 12 physics | boards neet in this video, we explore the concept of magnetic field on the axis of a.

Magnetic Field On The Axis Of A Circular Current Loop Evaluate The Magnetic Field Due To A It can be resolved into two components, one is vertical component of magnitude $db\: sin\phi$ along the axis of the loop and the other is horizontal component of magnitude $db\: cos\phi$ at right angles to the axis. 🔴 magnetic field at the axis of a circular current carrying loop | class 12 physics | boards neet in this video, we explore the concept of magnetic field on the axis of a. Moving charges & magnetism worksheets this worksheet is based on magnetic field at center of circular current carrying loop. it includes questions from exams. Electric current in a circular loop creates a magnetic field which is more concentrated in the center of the loop than outside the loop. stacking multiple loops concentrates the field even more into what is called a solenoid. When the charged particle q moves with the velocity v in the magnetic field b and the velocity of the particle is perpendicular to the direction of the magnetic field then force acting on it is given by f = q (v × b). hence, the magnetic force is directed towards the circular motion of the particle and acts as a centripetal force. Today, we explore how magnetic fields are calculated, particularly the magnetic field on the axis of a circular current loop, using the biot savart law. can anyone recall what the biot savart law states? it's about how the magnetic field is produced by a current element? exactly!.
Magnetic Field On Axis Of Circular Loop Physics Vidyalay Moving charges & magnetism worksheets this worksheet is based on magnetic field at center of circular current carrying loop. it includes questions from exams. Electric current in a circular loop creates a magnetic field which is more concentrated in the center of the loop than outside the loop. stacking multiple loops concentrates the field even more into what is called a solenoid. When the charged particle q moves with the velocity v in the magnetic field b and the velocity of the particle is perpendicular to the direction of the magnetic field then force acting on it is given by f = q (v × b). hence, the magnetic force is directed towards the circular motion of the particle and acts as a centripetal force. Today, we explore how magnetic fields are calculated, particularly the magnetic field on the axis of a circular current loop, using the biot savart law. can anyone recall what the biot savart law states? it's about how the magnetic field is produced by a current element? exactly!.
Comments are closed.