Onto Functions In Mathematics Geeksforgeeks

Functions Introduction One To Onto Surjection Bijective Identity Inverse Composition In simple words, for any function, if all the elements of the codomain are mapped to some element of the domain, then the function is said to be an onto function. in this article, we will discuss the concept of onto or surjective function in detail including its definition, example, and many more. In this article, the concept of the onto function, which is also called a surjective function, is discussed. also, learn about its definition, the way to find out the number of onto functions and how to prove whether a function is surjective with the help of examples.
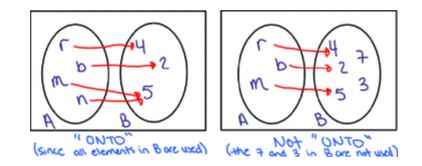
One To One And Onto Functions Nool Onto function is a function f that maps an element x to every element y. that means, for every y, there is an x such that f (x) = y. onto function is also called surjective function. the concept of onto function is very important while determining the inverse of a function. In mathematics, a surjective function (also known as surjection, or onto function ˈ ɒ n. t uː ) is a function f such that, for every element y of the function's codomain, there exists at least one element x in the function's domain such that f(x) = y. Onto function (surjective): every element in the codomain is mapped by at least one element from the domain. bijective function: a function that is both one to one and onto. objective function: this is not a type of function in mathematics; it refers to a function used in optimization problems. Onto function is one of the many types of functions defined based on the relationship between its domain and codomain. for any function to be onto, it needs to relate two sets with a very specific mapping between elements, meaning that each element of the codomain has at least one element in the domain as its pre image.
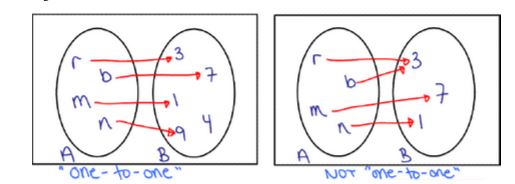
One To One And Onto Functions Nool Onto function (surjective): every element in the codomain is mapped by at least one element from the domain. bijective function: a function that is both one to one and onto. objective function: this is not a type of function in mathematics; it refers to a function used in optimization problems. Onto function is one of the many types of functions defined based on the relationship between its domain and codomain. for any function to be onto, it needs to relate two sets with a very specific mapping between elements, meaning that each element of the codomain has at least one element in the domain as its pre image. These notes cover functions, including function composition and when a function is onto. this topic includes discussion of nested (dissimilar) quan tifiers. we’re all familiar with functions from high school and calculus. In this method, we check for each and every element manually if it has unique image. check whether the following are onto? since all elements of set b has a pre image in set a, it is onto. since all elements of set b has a pre image in set a, it is onto. since element b has no pre image, it is not onto. since element e has no pre image,. In the above figure, f is an onto function. example 1 : check whether the following function is onto. f : n → n defined by f (n) = n 2. solution : domain and co domains are containing a set of all natural numbers. if x = 1, then f (1) = 1 2 = 3. if x = 2, then f (2) = 2 2 = 4. Onto functions focus on the codomain. we want to know if it contains elements not associated with any element in the domain. a function f: a → b is onto if, for every element b ∈ b, there exists an element a ∈ a such that f(a) = b. an onto function is also called a surjection, and we say it is surjective.
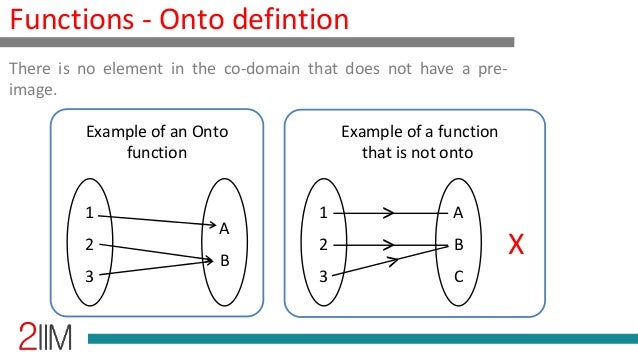
Onto Functions These notes cover functions, including function composition and when a function is onto. this topic includes discussion of nested (dissimilar) quan tifiers. we’re all familiar with functions from high school and calculus. In this method, we check for each and every element manually if it has unique image. check whether the following are onto? since all elements of set b has a pre image in set a, it is onto. since all elements of set b has a pre image in set a, it is onto. since element b has no pre image, it is not onto. since element e has no pre image,. In the above figure, f is an onto function. example 1 : check whether the following function is onto. f : n → n defined by f (n) = n 2. solution : domain and co domains are containing a set of all natural numbers. if x = 1, then f (1) = 1 2 = 3. if x = 2, then f (2) = 2 2 = 4. Onto functions focus on the codomain. we want to know if it contains elements not associated with any element in the domain. a function f: a → b is onto if, for every element b ∈ b, there exists an element a ∈ a such that f(a) = b. an onto function is also called a surjection, and we say it is surjective.

Onto Functions In the above figure, f is an onto function. example 1 : check whether the following function is onto. f : n → n defined by f (n) = n 2. solution : domain and co domains are containing a set of all natural numbers. if x = 1, then f (1) = 1 2 = 3. if x = 2, then f (2) = 2 2 = 4. Onto functions focus on the codomain. we want to know if it contains elements not associated with any element in the domain. a function f: a → b is onto if, for every element b ∈ b, there exists an element a ∈ a such that f(a) = b. an onto function is also called a surjection, and we say it is surjective.

Functions In Discrete Mathematics Geeksforgeeks
Comments are closed.