Relative Extrema Local Maximum And Minimum First Derivative Test Critical Points Calculus

6 9 First Derivative Test For Local Extrema Avidemia This calculus video tutorial explains how to find the relative extrema of a function such as the local maximum and minimum values using the first derivative. In this section we are going to be looking at identifying relative minimums and relative maximums. recall as well that we will often use the word extrema to refer to both minimums and maximums.

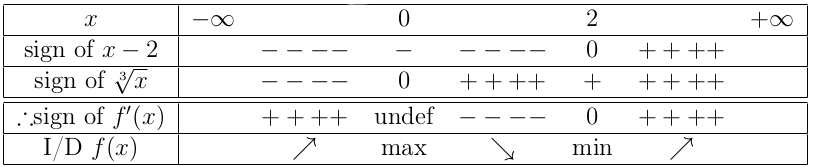
6 9 First Derivative Test For Local Extrema Avidemia The first derivative test is a central idea in calculus for identifying local (relative) extrema. it explains when a function stops climbing and starts descending (local maximum) or when it transitions from falling to rising (local minimum). State the first derivative test for critical points. find local extrema using the first derivative test. Once you find a critical point, how can you tell if it is a minimum, maximum or neither?. Mathematically, we can derive the first derivative test to find the local maxima and local minima of a function using the critical point and the first derivative of the function. suppose f is a function defined on an open interval i and continuous at a critical point c in i.

6 9 First Derivative Test For Local Extrema Avidemia Once you find a critical point, how can you tell if it is a minimum, maximum or neither?. Mathematically, we can derive the first derivative test to find the local maxima and local minima of a function using the critical point and the first derivative of the function. suppose f is a function defined on an open interval i and continuous at a critical point c in i. These are the critical points of f, so if f has any local extrema, they will happen at these points. we next apply the first derivative test to each of these critical points. this requires examining the sign change of f0(x) at each critical point. we use our familiar procedure of examining the factors of f0 ( x)=4 1)( °1). °1 0 1. The first derivative test works on the concept of approximation, which finds the local maxima and local minima by taking values from the left and from the right in the neighborhood of the critical points and substituting it in the expression of the first derivative. Solving f′(x) = 4x3 −6x2 = 0, we see that fhas two critical points, at x= 0 and x= 3 2. it looks like the critical point at x= 3 2 is a local minimum and the one at x= 0 is neither a minimum nor a maximum, but how can we know for sure? one way is just to compare the values at all the critical points. however, this doesn’t. First derivative test is a method used to analyze the critical points of a function and determine whether at that point function attains its maximum or minimum value. it is one of the basic tests in calculus which uses the change in slope to determine the extremum value of the function.

First Derivative Test And Local Extrema Ap Calculus Ab Bc Review Albert Resources These are the critical points of f, so if f has any local extrema, they will happen at these points. we next apply the first derivative test to each of these critical points. this requires examining the sign change of f0(x) at each critical point. we use our familiar procedure of examining the factors of f0 ( x)=4 1)( °1). °1 0 1. The first derivative test works on the concept of approximation, which finds the local maxima and local minima by taking values from the left and from the right in the neighborhood of the critical points and substituting it in the expression of the first derivative. Solving f′(x) = 4x3 −6x2 = 0, we see that fhas two critical points, at x= 0 and x= 3 2. it looks like the critical point at x= 3 2 is a local minimum and the one at x= 0 is neither a minimum nor a maximum, but how can we know for sure? one way is just to compare the values at all the critical points. however, this doesn’t. First derivative test is a method used to analyze the critical points of a function and determine whether at that point function attains its maximum or minimum value. it is one of the basic tests in calculus which uses the change in slope to determine the extremum value of the function.