Sinx N To Calculate The Value Of Sinx Using Its Taylor Series Expansion
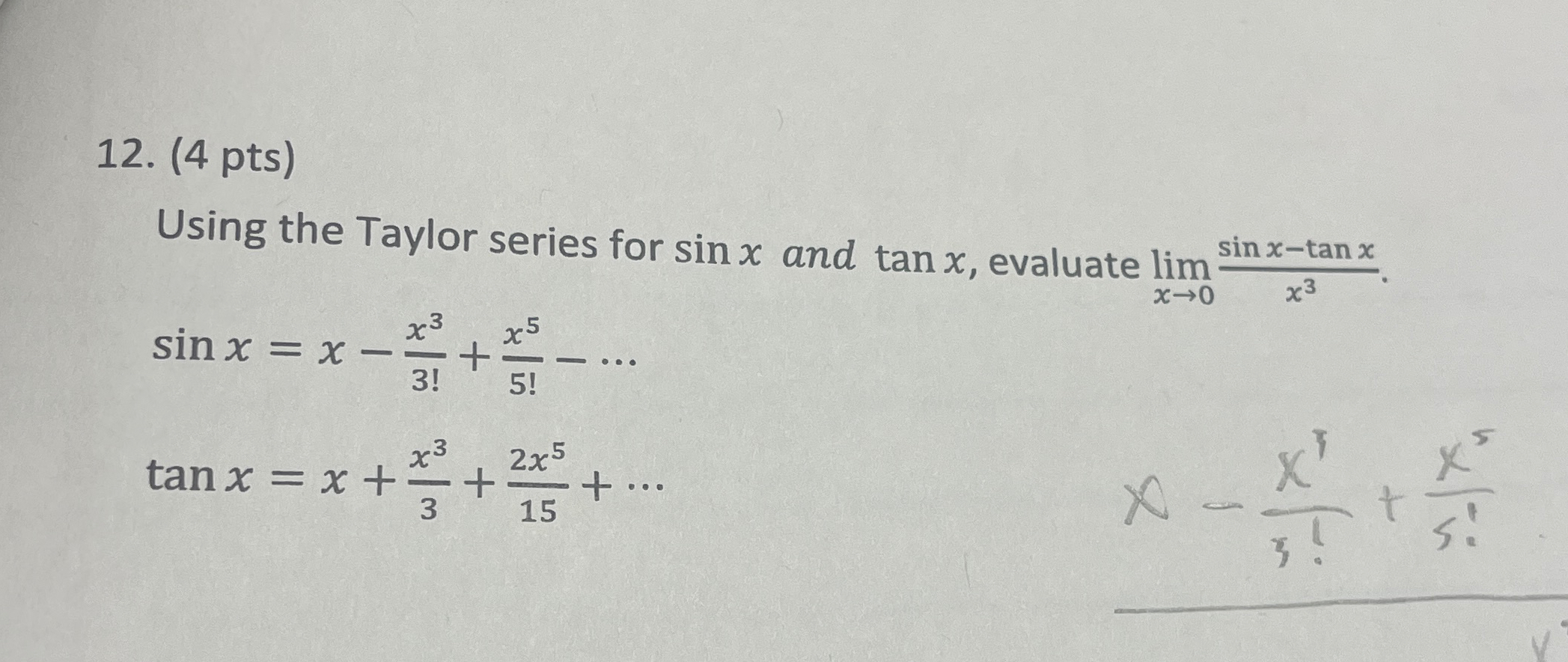
Solved 4 ï Pts Using The Taylor Series For Sinx ï And Tanx Chegg Given a value of angle, you need to calculate sin and cos values corresponding to it. for sin function. examples: x 3 3! x 5 5! {\displaystyle sin (x)=\sum {k=0}^ {\infty } \frac { ( 1)^k} { (2k 1)!}x^ {2k 1}=x \frac {x^3} {3!} \frac {x^5} {5!} } s in(x) = k=0∑∞ (2k 1)!(−1)k x2k 1 = x − 3!x3 5!x5 −. If we use enough terms of the series we can get a good estimate of the value of sin(x) for any value of x. this is very useful information about the function sin(x) but it doesn’t tell the whole story. for example, it’s hard to tell from the formula that sin(x) is periodic. the period of sin(x) is 2π; how is this series related to the.

Solved The Taylor Series For Sinx About X 0 Is Given By Chegg Calculate g(x) = sin(x) using the taylor series expansion for a given value of x. solve for g(pi 3) using 5, 10, 20 and 100 terms in the taylor series (use a loop). Free taylor series calculator find the taylor series representation of functions step by step. Take in the value of x in degrees and the number of terms and store it in separate variables. 2. pass these values to the sine function as arguments. 3. define a sine function and using a for loop, first convert degrees to radians. 4. then use the sine formula expansion and add each term to the sum variable. 5. The sin(x, n) function in python is defined to calculate the value of sin(x) using its taylor series expansion up to n terms. the function uses a loop to iterate from 0 to n, representing the number of terms to use in the taylor series expansion.

C Issue Regarding Calculation Of Sin X Using Taylor Series Stack Overflow Take in the value of x in degrees and the number of terms and store it in separate variables. 2. pass these values to the sine function as arguments. 3. define a sine function and using a for loop, first convert degrees to radians. 4. then use the sine formula expansion and add each term to the sum variable. 5. The sin(x, n) function in python is defined to calculate the value of sin(x) using its taylor series expansion up to n terms. the function uses a loop to iterate from 0 to n, representing the number of terms to use in the taylor series expansion. I am working on a python program in jupyter notebook that outputs the sum of a taylor series of sin(x) and e^x and compares them to the math module's output for a school assignment. the e^x portion seems to work fine, the output sum is close to the module calculation. Answer: the taylor (maclaurin) series of sin(x) sin (x) up to n = 5 n = 5 is sin(x) ≈ p(x) = x − 1 6x3 1 120x5 sin (x) ≈ p (x) = x 1 6 x 3 1 120 x 5. the calculator will find the taylor (or power) series expansion of the given function around the given point, with steps shown. We can use the first few terms of a taylor series to get an approximate value for a function. here we show better and better approximations for cos (x). the red line is cos (x), the blue is the approximation (try plotting it yourself) : 1 − x2 2! x4 4! − x6 6! x8 8!. Write a c program that calculates the value of sin(x) using the taylor series approximation. the program should prompt the user to enter the value of the angle x in radians and the number of terms n to include in the series.

Find The Taylor Series For F X Sinx ï About X 0 ï Up Chegg I am working on a python program in jupyter notebook that outputs the sum of a taylor series of sin(x) and e^x and compares them to the math module's output for a school assignment. the e^x portion seems to work fine, the output sum is close to the module calculation. Answer: the taylor (maclaurin) series of sin(x) sin (x) up to n = 5 n = 5 is sin(x) ≈ p(x) = x − 1 6x3 1 120x5 sin (x) ≈ p (x) = x 1 6 x 3 1 120 x 5. the calculator will find the taylor (or power) series expansion of the given function around the given point, with steps shown. We can use the first few terms of a taylor series to get an approximate value for a function. here we show better and better approximations for cos (x). the red line is cos (x), the blue is the approximation (try plotting it yourself) : 1 − x2 2! x4 4! − x6 6! x8 8!. Write a c program that calculates the value of sin(x) using the taylor series approximation. the program should prompt the user to enter the value of the angle x in radians and the number of terms n to include in the series.
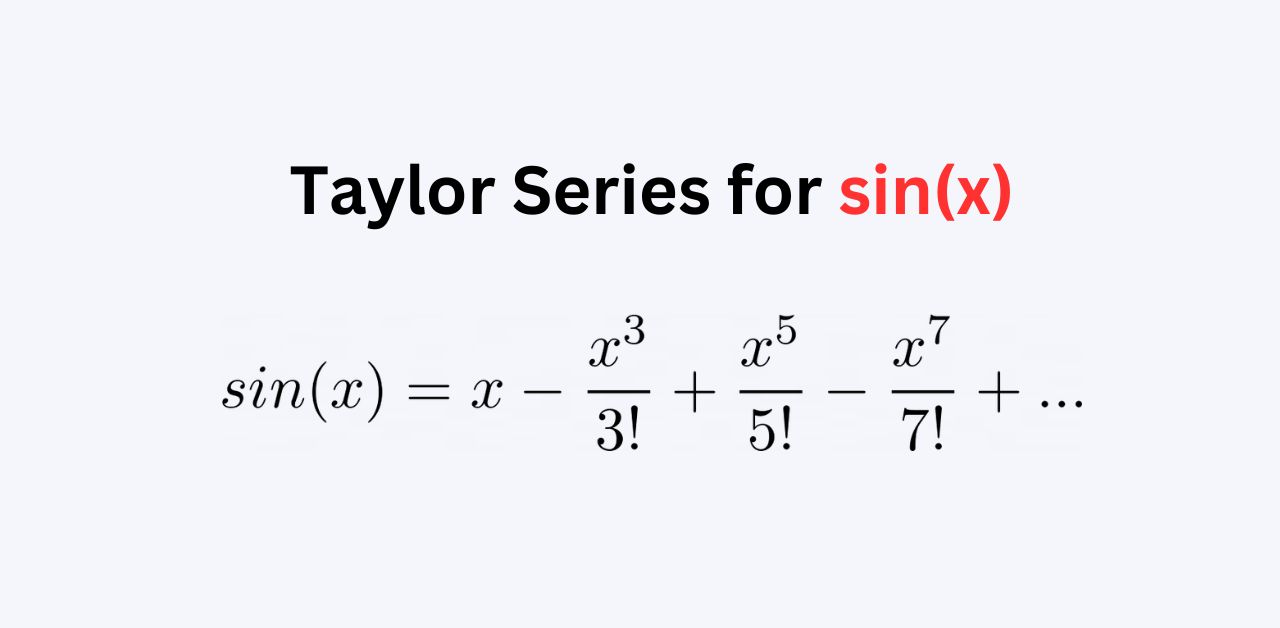
Taylor Series For Sinx We can use the first few terms of a taylor series to get an approximate value for a function. here we show better and better approximations for cos (x). the red line is cos (x), the blue is the approximation (try plotting it yourself) : 1 − x2 2! x4 4! − x6 6! x8 8!. Write a c program that calculates the value of sin(x) using the taylor series approximation. the program should prompt the user to enter the value of the angle x in radians and the number of terms n to include in the series.
Comments are closed.