Solve Exponential Equations Using Logarithms Studyx

Exponential Graphs And Using Logarithms To Solve Equations Pdf Logarithm Mathematical Objects Understanding the relationship between logarithms and exponentials is essential for simplifying logarithmic equations. always verify the solution by substituting the values back into the original equations. Learn the techniques for solving exponential equations that requires the need of using logarithms, supported by detailed step by step examples. this is necessary because manipulating the exponential equation to establish a common base on both sides proves to be challenging.
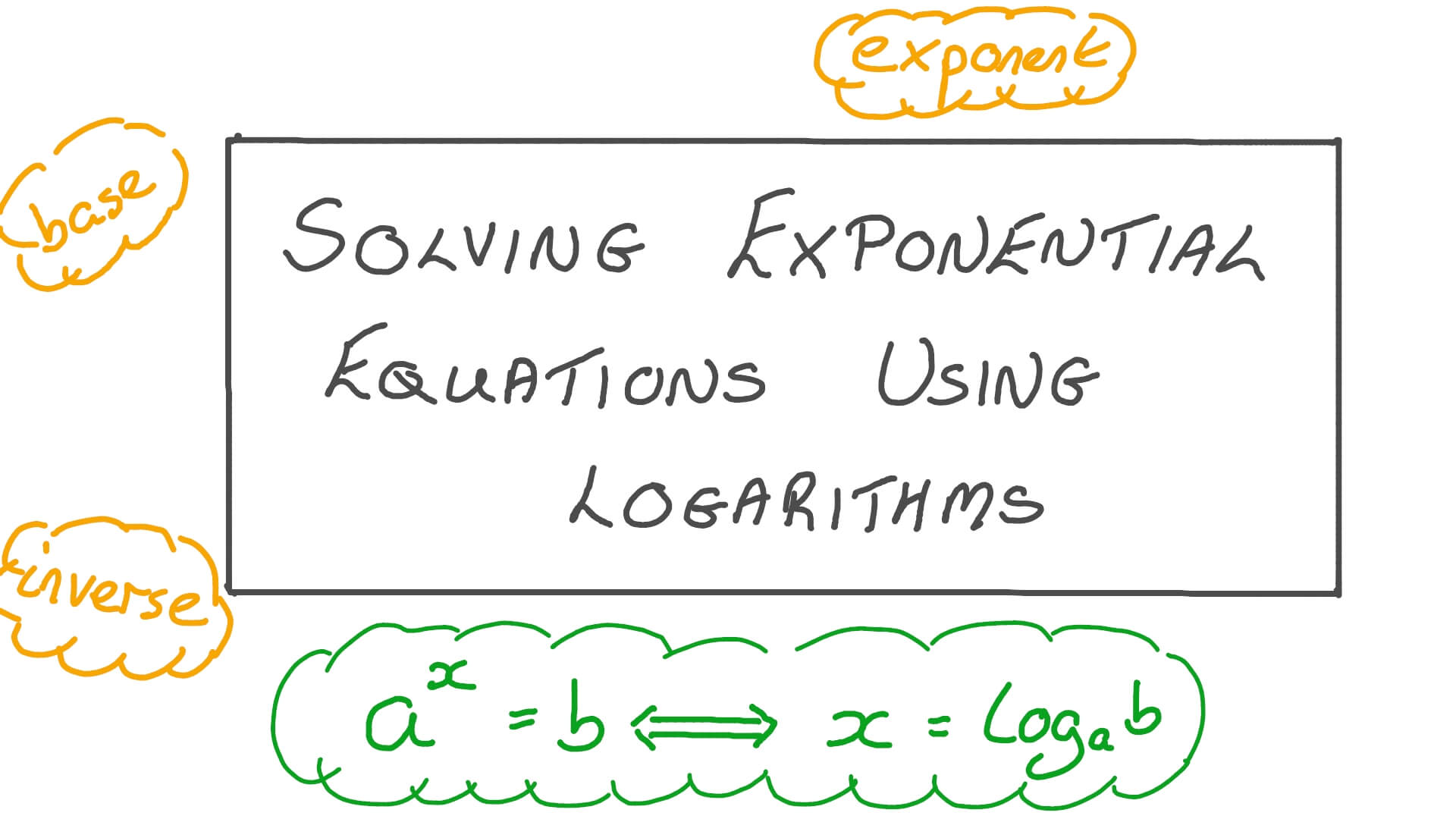
How To Solve Exponential Equations Without Logarithms Tessshebaylo Demonstrates how to solve exponential equations by using logarithms. explains how to recognize when logarithms are necessary. provides worked examples showing how to obtain "exact" answers. Use the method of common bases to solve exponential equations. use logarithms to solve exponential equations. use the definition of a logarithm to solve logarithmic equations. use the one to one property of logarithms to solve logarithmic equations. Use logarithms to solve exponential equations sometimes the terms of an exponential equation cannot be rewritten with a common base. in these cases, we solve by taking the logarithm of each side. 1 solve, we can adjust the equation by either taking the logarithm of both sides, or by exponentiating both sides (i.e. raising b to the power of each side) and still obtain a valid equation with the same set of solutions.

How To Solve Exponential Equations Using Logarithms Use logarithms to solve exponential equations sometimes the terms of an exponential equation cannot be rewritten with a common base. in these cases, we solve by taking the logarithm of each side. 1 solve, we can adjust the equation by either taking the logarithm of both sides, or by exponentiating both sides (i.e. raising b to the power of each side) and still obtain a valid equation with the same set of solutions. Ideas for solving the problem logarithm application: apply logarithms to both sides of the equation to bring down the exponents. power rule of logarithms: use the power rule, ln(ab) = b ⋅ln(a), to simplify the equation. algebraic manipulation: expand, rearrange, and factor to isolate the variable x. In this section, we will introduce logarithmic functions as a tool to solve exponential equations. we will also explore solving logarithmic equations and revisit modeling applications with …. The next step in solving exponential equations involves using their inverse, the logarithm. you will work with several different bases and even with exponents that are expressions. For the following exercises, solve each equation by rewriting the exponential expression using the indicated logarithm. then use a calculator to approximate x to 3 decimal places.
Comments are closed.