Solved 1 Consider The Series N In N N 2 Test The Series Chegg

Solved Consider The Series в N 1в ћan Where An N2 2n 2 в 1 Nn2 Chegg Answer to consider the following series. Σ ( ( 1)" n=2 in (5n). Free online series convergence calculator check convergence of infinite series step by step.

Solved Consider The Series в N 1в ћan Chegg 1. x∞ n=2 1 n √ lnn solution: the function 1 n √ lnn is decreasing and positive for n ≥ 2, then the integral test says that x∞ n=2 1 n √ lnn behaves as z∞ 2 1 x √ lnx dx. z∞ 2 1 x √ lnx dx= lim b→∞ z b 2 1 x √ lnx dx= lim b→∞ z lnb ln2 u−1 2du= lim b→∞ 2 √ u lnb ln2 = ∞. hence x∞ n=2 1 n √ lnn. Answer: this is an alternating series, so we need to check that the terms satisfy the hy potheses of the alternating series test. to see that the terms are decreasing in absolute value. f(x) = √ . \[\frac{{{n^2}}}{{{n^4}}} = \frac{1}{{{n^2}}}\] which will converge as a series. therefore, we can guess that the original series will converge and we will need to find a larger series which also converges. this means that we’ll either have to make the numerator larger or the denominator smaller. In this article, we will explore what a series is, how to work with them, and how the symbolab series calculator can support your learning. step by step, you will see how it all adds up. what is a series? a series is what happens when we take the terms of a sequence and add them together.

Solved Consider The Series в N 1в ћan Where An N2 4n 3 в 1 Nn2 Chegg \[\frac{{{n^2}}}{{{n^4}}} = \frac{1}{{{n^2}}}\] which will converge as a series. therefore, we can guess that the original series will converge and we will need to find a larger series which also converges. this means that we’ll either have to make the numerator larger or the denominator smaller. In this article, we will explore what a series is, how to work with them, and how the symbolab series calculator can support your learning. step by step, you will see how it all adds up. what is a series? a series is what happens when we take the terms of a sequence and add them together. 1. n b. n = (p series) 2. 2 1. 1. n a. n. ≤ = , and . ∑. ∞ =1 2. 1. n. n. converges, so by (i), ∑. ∞ =1 2 1. n n. n. converges. some series will “obviously” not converge—recognizing these can save you a lot of time and guesswork. test for divergence. if . lim ≠0 →. ∞. n n. a, then . ∑. ∞. n= 1. a n. is divergent. Series (2), shown in equation 5.12, is called the alternating harmonic series. we will show that whereas the harmonic series diverges, the alternating harmonic series converges. to prove this, we look at the sequence of partial sums {sk} {s k} (figure 5.17). Example 1 determine if the following series is convergent or divergent. if it converges determine its value. ∞ ∑ n=1n ∑ n = 1 ∞ n. to determine if the series is convergent we first need to get our hands on a formula for the general term in the sequence of partial sums. Tip: always check the nth term first, because the series and its positive term series diverge if the nth term is not zero. also, to tell whether a function decreases or increases, you can use the first derivative.
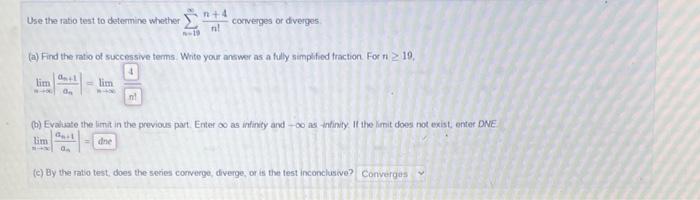
Solved Consider The Series в I 1в ћan Where An N2 2n 2 в 1 Nn2 Chegg 1. n b. n = (p series) 2. 2 1. 1. n a. n. ≤ = , and . ∑. ∞ =1 2. 1. n. n. converges, so by (i), ∑. ∞ =1 2 1. n n. n. converges. some series will “obviously” not converge—recognizing these can save you a lot of time and guesswork. test for divergence. if . lim ≠0 →. ∞. n n. a, then . ∑. ∞. n= 1. a n. is divergent. Series (2), shown in equation 5.12, is called the alternating harmonic series. we will show that whereas the harmonic series diverges, the alternating harmonic series converges. to prove this, we look at the sequence of partial sums {sk} {s k} (figure 5.17). Example 1 determine if the following series is convergent or divergent. if it converges determine its value. ∞ ∑ n=1n ∑ n = 1 ∞ n. to determine if the series is convergent we first need to get our hands on a formula for the general term in the sequence of partial sums. Tip: always check the nth term first, because the series and its positive term series diverge if the nth term is not zero. also, to tell whether a function decreases or increases, you can use the first derivative.
Comments are closed.