Solved 6 Let G %d0%b2 Be A Group And A B C%d0%b2 G A Prove If Chegg

Solved A Let G Be A Group With Binary Operation And Set Chegg There are 2 steps to solve this one. 6. let g be a group and a,b ∈g. prove the following. (1) o(a)=o(a−1) (2) o(aba−1)=o(b). not the question you’re looking for? post any question and get expert help quickly. answer to 6. let g be a group and a,b∈g. prove the following. Suppose that two elements a and b in a group g commute, and suppose that am = e = b n . show that (ab) k = e, where k = lcm(m,n), the least common multiple of m and n.

Solved 4 Let G A B2 A Bв Q A Prove That G Is A Group Chegg A) prove that if a ∈ g has finite order n then, for any integer k, the order of ak is n gcd(n,k). b) suppose that a ∈ g has order m and b ∈ g has order n. Let a and b belong to a group g. find an x in g such that xabx 1 = ba. solution: it is equivalent to show xabx 1 a 1 = b, since we have b’s in the center of both expressions, one easy way to make them equal is to let xa = e, or x = a 1 . You need to prove your claim that g g is closed under ∗ ∗, not just state it. for what it is worth, this is an example of a semidirect product of groups. in this case, for each element of r =r0 r = r 0, we hav an automorphism ϕr ϕ r of (r, ) (r, ) defined as ϕr(x) = r2x ϕ r (x) = r 2 x. We have shown that if ab = ac for elements a, b, and c in a group g, then b = c. we used the properties of a group, including the existence of inverses and the identity element, to prove this result.

Solved 2 Let G Be A Group And Let A B Cв G A Using Only Chegg You need to prove your claim that g g is closed under ∗ ∗, not just state it. for what it is worth, this is an example of a semidirect product of groups. in this case, for each element of r =r0 r = r 0, we hav an automorphism ϕr ϕ r of (r, ) (r, ) defined as ϕr(x) = r2x ϕ r (x) = r 2 x. We have shown that if ab = ac for elements a, b, and c in a group g, then b = c. we used the properties of a group, including the existence of inverses and the identity element, to prove this result. Similarly, u ∈ b and since b is a subgroup of g, u−1 ∈ b. therefore, u −1 ∈ c. we have proved the three things that are needed to verify that c is a subgroup of g. [optional question] let g be a group and let a ∈ g. prove that for any integers n, m ∈ z, we have anam = an m. [suggestion: fix m ∈ z and show that this works for n = 0 and n = 1, then prove it by induction on n for n ≥ 1. finally, think about what happens when n < 0.] solution if n = 0 then an = e so anam = am and an m = am. so this works. The hypothesis implies an exponent of two for the group. but then it is abelian, since $ab=(ab)^{ 1}=b^{ 1}a^{ 1}=ba$, for any two elements of the group $a$ and $b$. So we only need to prove that ϕ−1 is a group homomorphism. to that end, let a0,b0 ∈ g0. then since ϕ is bijective, there exist a,b ∈ g with ϕ(a) = a0 and ϕ(b) = b0, i.e. a = ϕ−1(a0) and b = ϕ−1(b0). now we have ϕ−1(a0b0) = ϕ−1(ϕ(a)ϕ(b)) = ϕ−1(ϕ(ab)) = ab = ϕ−1(a0)ϕ−1(b0),.

Solved Let G Be A Group A B C G Prove в јabcв ј в јbcaв ј в јcabв ј Chegg Similarly, u ∈ b and since b is a subgroup of g, u−1 ∈ b. therefore, u −1 ∈ c. we have proved the three things that are needed to verify that c is a subgroup of g. [optional question] let g be a group and let a ∈ g. prove that for any integers n, m ∈ z, we have anam = an m. [suggestion: fix m ∈ z and show that this works for n = 0 and n = 1, then prove it by induction on n for n ≥ 1. finally, think about what happens when n < 0.] solution if n = 0 then an = e so anam = am and an m = am. so this works. The hypothesis implies an exponent of two for the group. but then it is abelian, since $ab=(ab)^{ 1}=b^{ 1}a^{ 1}=ba$, for any two elements of the group $a$ and $b$. So we only need to prove that ϕ−1 is a group homomorphism. to that end, let a0,b0 ∈ g0. then since ϕ is bijective, there exist a,b ∈ g with ϕ(a) = a0 and ϕ(b) = b0, i.e. a = ϕ−1(a0) and b = ϕ−1(b0). now we have ϕ−1(a0b0) = ϕ−1(ϕ(a)ϕ(b)) = ϕ−1(ϕ(ab)) = ab = ϕ−1(a0)ϕ−1(b0),.
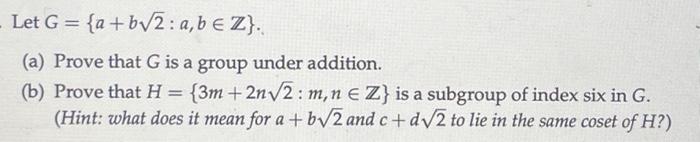
Solved Let G A B2 A Bв Z A Prove That G Is A Group Under Chegg The hypothesis implies an exponent of two for the group. but then it is abelian, since $ab=(ab)^{ 1}=b^{ 1}a^{ 1}=ba$, for any two elements of the group $a$ and $b$. So we only need to prove that ϕ−1 is a group homomorphism. to that end, let a0,b0 ∈ g0. then since ϕ is bijective, there exist a,b ∈ g with ϕ(a) = a0 and ϕ(b) = b0, i.e. a = ϕ−1(a0) and b = ϕ−1(b0). now we have ϕ−1(a0b0) = ϕ−1(ϕ(a)ϕ(b)) = ϕ−1(ϕ(ab)) = ab = ϕ−1(a0)ϕ−1(b0),.

Solved Let G Be A Group And Let A Bв G Such That Ab Ba Chegg
Comments are closed.