Solved A Batsman Hits Back A Ball Of Mass 0 15 Kg Straight In The Direction Of The Bowler

A Batsman Hits Back A Ball Of Mass 0 15 Kg Straight In The Direction Of T Here mass of the ball is given as 0.15kg and the initial velocity of the ball before hitting the bat is 12 m s 1. after hitting the ball it was given that the magnitude of velocity is the same but the direction of velocity is reversed. A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12ms−1 . if the mass of the ball is 0.15 kg , determine the impulse imparted to the ball .

Answered 22 A Batsman Hits Back A Ball Of Mass 0 15 Kg Straight In Kunduz A batsman hits back a ball of mass 0.15 kg straight in the direction of the bowler without changing its initial speed of 12 m s^ 1. A batsman hits back a ball of mass 0.15 kg straight in the directionof the bowler without changing its initial… get the answers you need, now!. Initial momentum of the ball = mass * initial velocity = 0.15 kg * 10 m s = 1.5 kg m s. final momentum of the ball = mass * final velocity = 0.15 kg * ( 10 m s) = 1.5 kg m s (since the ball is moving in the opposite direction). Now we have to find the impulse imported to this ball, as we considered in both imparted to the ball is given by that is equal to change in momentum of this ball.

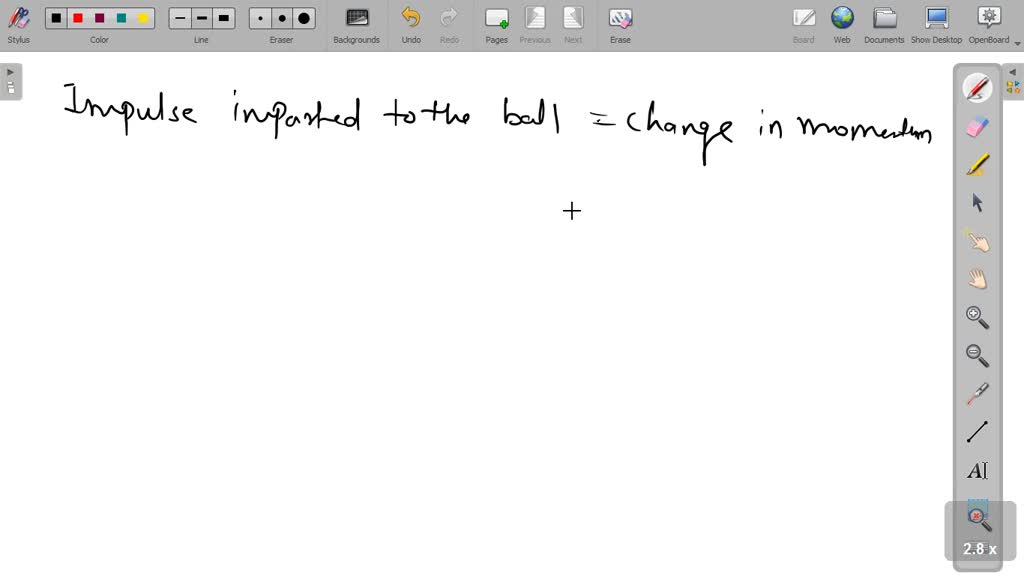
Solved A Batsman Hits Back A Ball Of Mass 0 15 Kg Straight In The Direction Of The Bowler Initial momentum of the ball = mass * initial velocity = 0.15 kg * 10 m s = 1.5 kg m s. final momentum of the ball = mass * final velocity = 0.15 kg * ( 10 m s) = 1.5 kg m s (since the ball is moving in the opposite direction). Now we have to find the impulse imported to this ball, as we considered in both imparted to the ball is given by that is equal to change in momentum of this ball. B 2.8n s c 3.6n s d 4.2n s solution: change in momentum = 0.15 ×12 −(−0.15 ×12) = 3.6n s impulse = 3.6n s in the direction from the batsman to the bowler. A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 m s−1. if the mass of the ball is 0.15 kg, determine the impulse imparted to the ball. To find the impulse imparted on the ball by the batsman, we can follow these steps: impulse is defined as the change in momentum of an object. mathematically, it can be expressed as: where pf is the final momentum and pi is the initial momentum. A batsman hits back a ball of mass 0.15 kg straight in the direction of the bowler without changing its initial speed of 12ms^ { 1} 12ms−1. if the ball moves linearly, then the impulse imparted to the ball is.

A Batsman Hits Back A Ball Of Mass 0 15 Kg Straight In The Direction Of The Bowler Without B 2.8n s c 3.6n s d 4.2n s solution: change in momentum = 0.15 ×12 −(−0.15 ×12) = 3.6n s impulse = 3.6n s in the direction from the batsman to the bowler. A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 m s−1. if the mass of the ball is 0.15 kg, determine the impulse imparted to the ball. To find the impulse imparted on the ball by the batsman, we can follow these steps: impulse is defined as the change in momentum of an object. mathematically, it can be expressed as: where pf is the final momentum and pi is the initial momentum. A batsman hits back a ball of mass 0.15 kg straight in the direction of the bowler without changing its initial speed of 12ms^ { 1} 12ms−1. if the ball moves linearly, then the impulse imparted to the ball is.

5 A Batsman Hits Back A Ball Of Mass 0 2 Kg Straight In The Direction Of To find the impulse imparted on the ball by the batsman, we can follow these steps: impulse is defined as the change in momentum of an object. mathematically, it can be expressed as: where pf is the final momentum and pi is the initial momentum. A batsman hits back a ball of mass 0.15 kg straight in the direction of the bowler without changing its initial speed of 12ms^ { 1} 12ms−1. if the ball moves linearly, then the impulse imparted to the ball is.