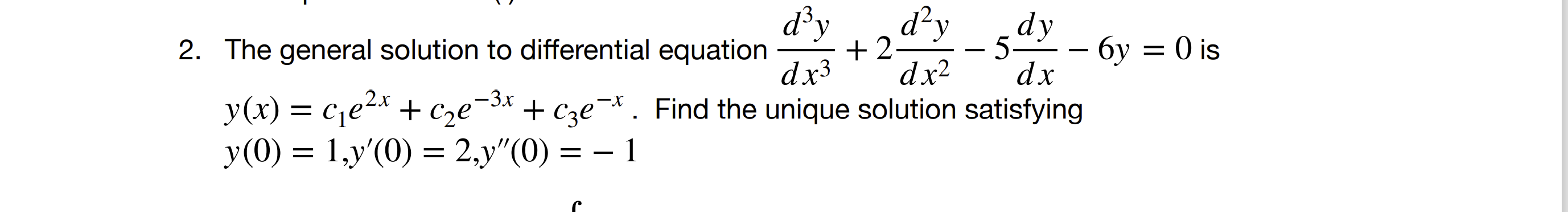
Solved A First Course In Differential Equations Chapter Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. Access study documents, get answers to your study questions, and connect with real tutors for math 2420 : differential equations with applications at university of texas, dallas.
Solved A Problems From A First Course In Differential Chegg Solutions manual for zill's differential equations textbooks (11th & 9th editions). includes solutions for modeling applications and boundary value problems. Solving for ygives y(t) = 1 2 (−1 √ 9 4t). the plus sign on the radical is taken to satisfy the initial condition. the solution exists for t>−9 4. 3. These are my solutions to the eleventh edition of a first course in differential equations with modeling applications by zill. it also includes the boundary value problem chapters from the ninth edition. Now, with expert verified solutions from a first course in differential equations with modeling applications 10th edition, you’ll learn how to solve your toughest homework problems.
Solved A Problems From A First Course In Differential Chegg These are my solutions to the eleventh edition of a first course in differential equations with modeling applications by zill. it also includes the boundary value problem chapters from the ninth edition. Now, with expert verified solutions from a first course in differential equations with modeling applications 10th edition, you’ll learn how to solve your toughest homework problems. Using the quadratic formula to solve y2 − 2x2y − 1 = 0 for y, we get y = 2x2 ± √ 4x4 4 2 = x2 ± √ x4 1. thus, two explicit solutions are y 1 = x2 √ x4 1 and y 2 = x2 − √ x4 1. both solutions are defined on (−∞,∞). the graph of y 1(x) is solid and the graph of y 2 is dashed. – 4 –2 2 4 x – 4 –2 2 4 y. A first course in differential equations with modeling applications, 12th edition , dennis zill, brooks cole publishing, 2024 your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. Access the complete solution set for zill’s a first course in differential equations with modeling applications (11th edition). Whenever you have a linear equation, you can always solve it using the method of integrating factors. put in standard form: y′ p(t)y = g(t). multiply by μ. find μ to match the product rule. reverse the product rule. integrate both sides and solve for y.
Comments are closed.