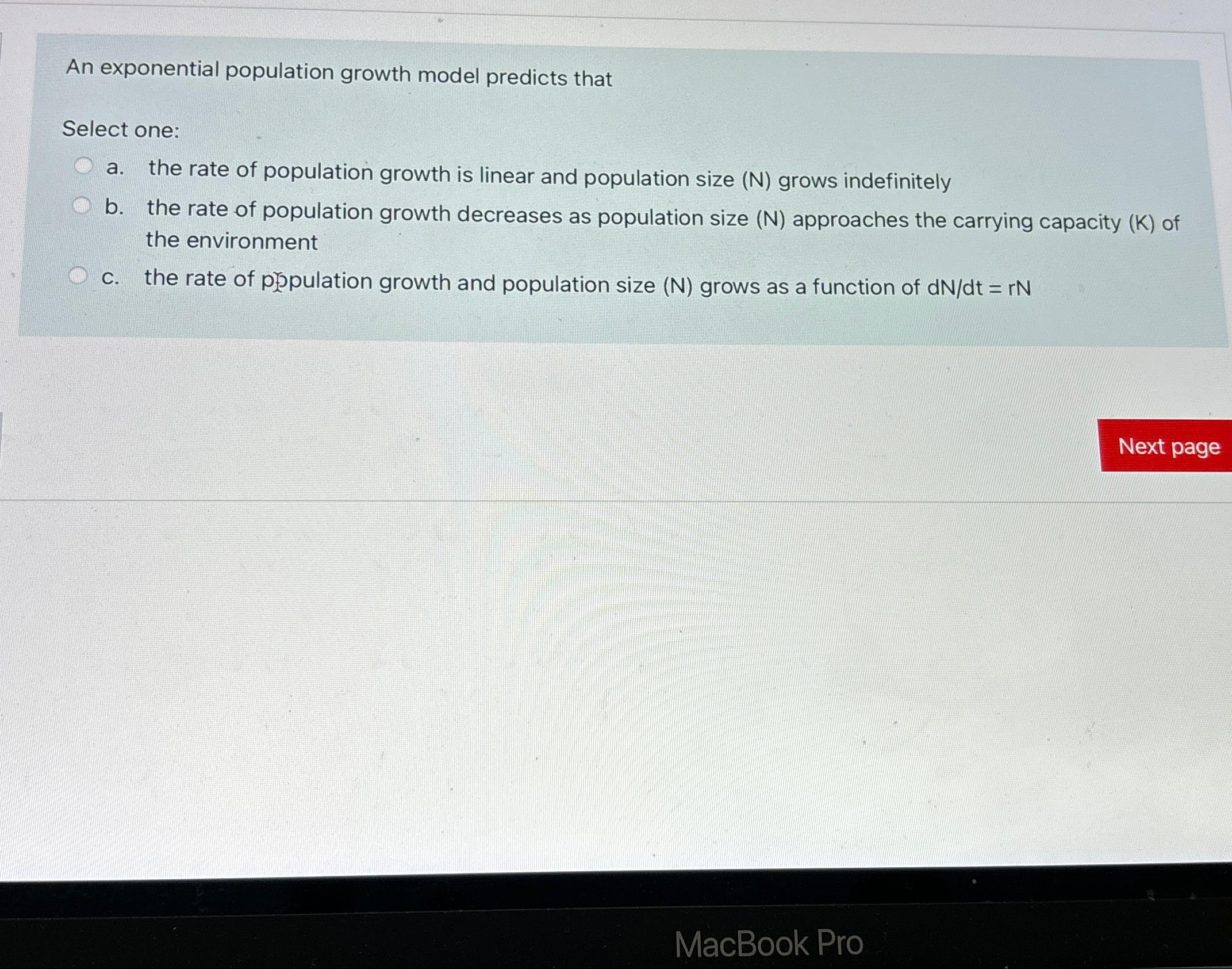
Solved An Exponential Population Growth Model Predicts Chegg Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. let's analyze what an exponential population growth model pre not the question you’re looking for? post any question and get expert help quickly. Problem: using the doubling time growth model, what will the population for a city be in 4 years if the current population is 750,000 and the doubling time is 36 years?.
Solved The Exponential Model Of Population Growth Predicts Chegg The formula for population growth of several species is the same as that for continuously compounded interest. in fact in both cases the rate of growth r of a population (or an investment) per time period is proportional to the size of the population (or the amount of an investment). In exponential growth, the population grows proportional to the size of the population, so as the population gets larger, the same percent growth will yield a larger numeric growth. But if you are given a question and not speci cally asked to do either of those two things, you can just memorize the fact that p(t) is the solution to the logistic growth di erential equation. So far, we have determined the exponential rate of growth for continuous time but we have not developed the equation for predicting population size in continuous time.
Solved The Exponential Model Of Population Growth Predicts Chegg But if you are given a question and not speci cally asked to do either of those two things, you can just memorize the fact that p(t) is the solution to the logistic growth di erential equation. So far, we have determined the exponential rate of growth for continuous time but we have not developed the equation for predicting population size in continuous time. Strictly speaking, the discrete time model represents geometric population growth. later in the exercise, we will develop a continuous time model, properly called an exponential model. many textbooks present only the continuous time exponential model. The model of exponential population growth assumes that the per capita population growth rate, often denoted as r, remains constant regardless of the population size. As to the exponential model predicts that p (t) — but the logistic model predicts that p (t) → k. both models have been used extensively to model a number of different populations, including bacteria, animals, fish, and human populations. The exponential growth model states that a population will grow exponentially if 1) births > deaths 2) if there are no other limitations on population growth (population size depends only on births and deaths) delta n = b d (if this is not the case, population will exponentially decline).
Comments are closed.