Solved Consider The Graph G V E Which Is Constructed By Chegg

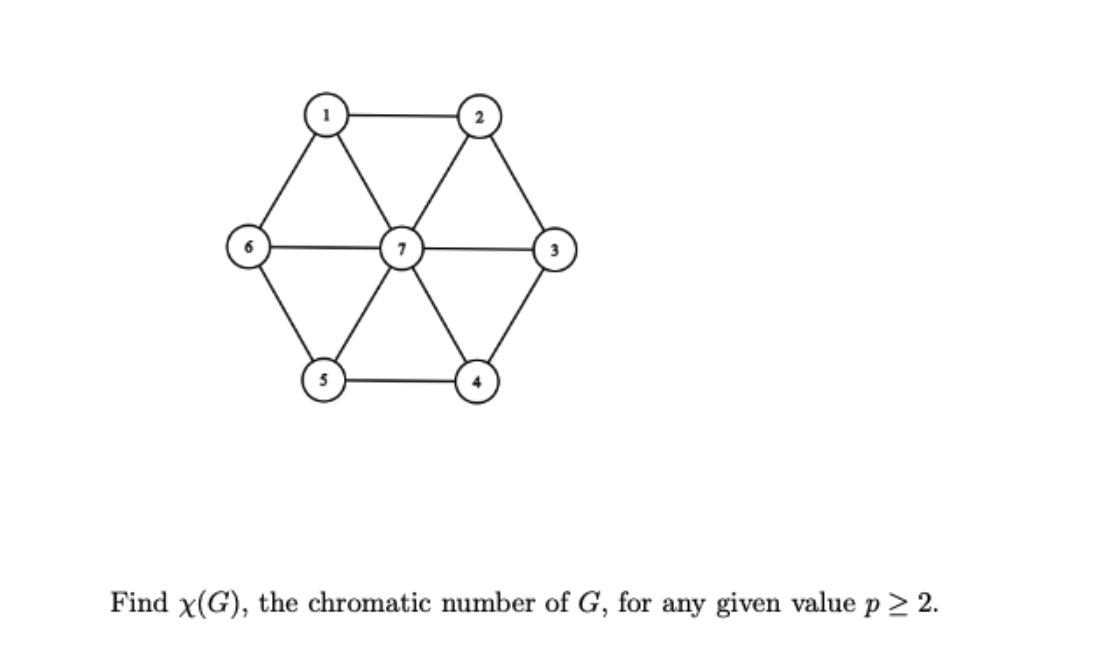
Solved Consider The Graph G V E Which Is Constructed By Chegg Consider the graph g= (v,e), which is constructed by taking the cycle graph c2p,p≥2, and adding a node which is adjacent to all other nodes. as an example, we have provided you the graph for p=3. find χ (g), the chromatic number of g, for any given value p≥2. your solution’s ready to go!. Given graph g have a perfect matching? this can be solved in polynomial time which is a fundamental result in combinatorial optimization with m. ny applications in theory and practice. it turns out that the perfectmatching problem.

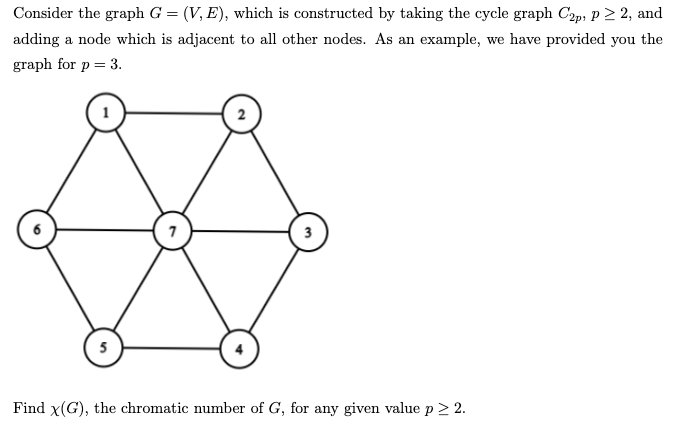
Solved Consider The Graph G V E Which Is Constructed By Chegg Let g =(v, e) be a connected, weighted undirected graph whose edges weight may or may not be distinct. given a cut (s, v − s) of s, recall that an edge (u, v) ∈ e is said to cross the cut. Consider the graph $g = (v, e)$, which is constructed by taking the cycle graph $c {2p}$, $p \geq 2$, and adding a node which is adjacent to all other nodes. find $\chi(g)$, the chromatic number of $g$, for any given value $p \geq 2$. Let u∗ u ∗ be a vc set for g that has the smallest size possible (meaning there does not exist any other vc set u u such that (| u u | < | u∗ u ∗ |). a subset w ⊆ v of the vertices of g is called an in set if for all i, j ∈ w, {i, j} ∉ ∉ e. Statement 1: given a graph g = (v, e) in which each vertex v ∈ v has an associated positive weight w(v), we can use linear programming to find the lower bound on the weight of the minimum weight vertex cover.

Solved Consider The Graph G V E Which Is Constructed By Chegg Let u∗ u ∗ be a vc set for g that has the smallest size possible (meaning there does not exist any other vc set u u such that (| u u | < | u∗ u ∗ |). a subset w ⊆ v of the vertices of g is called an in set if for all i, j ∈ w, {i, j} ∉ ∉ e. Statement 1: given a graph g = (v, e) in which each vertex v ∈ v has an associated positive weight w(v), we can use linear programming to find the lower bound on the weight of the minimum weight vertex cover. We are given an undirected graph g = (v, e) where each edge e has weight w(e) 0. the goal is to find a cut s ˆv that maximizes the total weight of cut edges. To create graph g'' that is not isomorphic to g, ensure that g'' has a different structure or vertex degree sequence. for example, g'' could be a chain of 7 vertices, which would have a degree sequence of 2, 2, 1, 1, 1, 1, 1. Consider the graph g = (v, e), which is constructed by taking the cycle graph c2p, p ≥ 2, and adding a node which is adjacent to all other nodes. find the chromatic number of g, for any given value p ≥ 2. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Explain why at least three edges have to be added to $g$ (while maintaining the node set) so that the block graph of the resulting graph consists of exactly one isolated point. give three edges that accomplish this.

Solved Consider A Graph G V E Where в јeв ј 2в јvв ј 24 Graph G Chegg We are given an undirected graph g = (v, e) where each edge e has weight w(e) 0. the goal is to find a cut s ˆv that maximizes the total weight of cut edges. To create graph g'' that is not isomorphic to g, ensure that g'' has a different structure or vertex degree sequence. for example, g'' could be a chain of 7 vertices, which would have a degree sequence of 2, 2, 1, 1, 1, 1, 1. Consider the graph g = (v, e), which is constructed by taking the cycle graph c2p, p ≥ 2, and adding a node which is adjacent to all other nodes. find the chromatic number of g, for any given value p ≥ 2. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Explain why at least three edges have to be added to $g$ (while maintaining the node set) so that the block graph of the resulting graph consists of exactly one isolated point. give three edges that accomplish this.