Solved Exercise 2 1 For Each Of The Following Functions F Chegg

Solved For The Following Exercise Given The Function F Chegg Question: exercise 2.1 for each of the following functions f sketch the graph y=f(x) in r 2. decide whethe the inverse function f−1 exists, and if it does exist write down the formula for f−1(y). f(x)=5x;f(x)=x2−4x 8;f(x)=x5. For each function f (n) f (n) and time t t in the following table, determine the largest size n n of a problem that can be solved in time t t, assuming that the algorithm to solve the problem takes f (n) f (n) microseconds. i wrote running time compare.py to solve this table.

Solved Exercise 3 1 For Each Of The Following Functions A Chegg For the exercises 68 73, evaluate the function \(f\) at the values \(f(−2)\), \(f(−1)\), \(f(0)\), \(f(1)\),and \(f(2)\). 68) \(f(x)=4−2x\) 69) \(f(x)=8−3x\). Determine the critical points of each of the following functions. \(f\left( x \right) = 8{x^3} 81{x^2} 42x 8\) solution \(r\left( t \right) = 1 80{t^3} 5{t^4} 2{t^5}\) solution. Now, with expert verified solutions from calculus, volume 2 1st edition, you’ll learn how to solve your toughest homework problems. our resource for calculus, volume 2 includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. Here’s the best way to solve it. exercise 2.1 for each of the following functions f sketch the graph y f (x) in r2. decide whether the inverse function f exists, and if it does exist write down the formula for f (y) not the question you’re looking for? post any question and get expert help quickly.
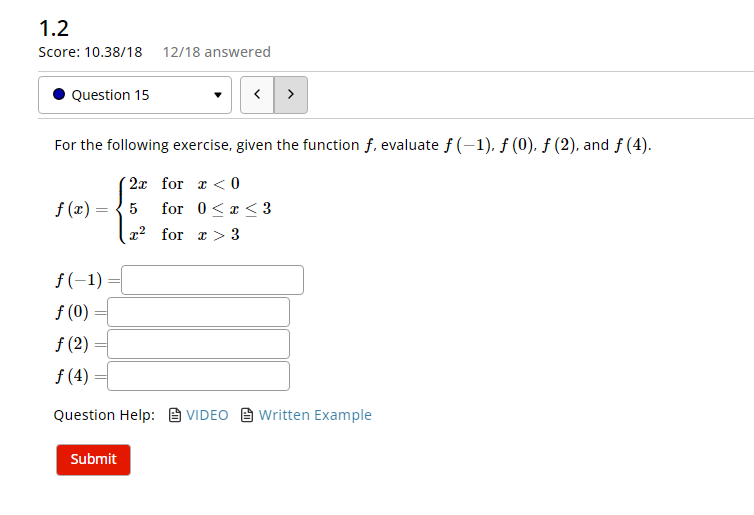
Solved For The Following Exercise Given The Function F Chegg Now, with expert verified solutions from calculus, volume 2 1st edition, you’ll learn how to solve your toughest homework problems. our resource for calculus, volume 2 includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. Here’s the best way to solve it. exercise 2.1 for each of the following functions f sketch the graph y f (x) in r2. decide whether the inverse function f exists, and if it does exist write down the formula for f (y) not the question you’re looking for? post any question and get expert help quickly. Problem 1: for each of the following functions do the following: (i) write the function as a piecewise function and sketch its graph, (ii) write the function as a combination of terms of the form u a(t)k(t a) and compute the laplace transform (a) f(t) = t(1 u 1(t)) et(u 1(t) u 2(t)) (b) h(t) = sin(2t) u ˇ(t)(t=ˇ sin(2t)) u 2ˇ(t)(2ˇ t)=ˇ. If the resulting function is the same as the original function, \(f(−x)=f(x)\), then the function is even. if the resulting function is the opposite of the original function, \(f(−x)=−f(x)\), then the original function is odd. A function as taking things from x, and sending them over to y, where the function f is the map that explains where each element in xis supposed to go. this is visualized in figure 1. For the following exercises, for each pair of functions, find a. \(f g\) b. \(f−g\) c. \(f⋅g\) d. \(f g\). determine the domain of each of these new functions. 1) \(f(x)=3x 4,g(x)=x−2\) 2) \(f(x)=x−8,g(x)=5x^2\).

Solved Problem 1 For Each Of The Following Functions F Chegg Problem 1: for each of the following functions do the following: (i) write the function as a piecewise function and sketch its graph, (ii) write the function as a combination of terms of the form u a(t)k(t a) and compute the laplace transform (a) f(t) = t(1 u 1(t)) et(u 1(t) u 2(t)) (b) h(t) = sin(2t) u ˇ(t)(t=ˇ sin(2t)) u 2ˇ(t)(2ˇ t)=ˇ. If the resulting function is the same as the original function, \(f(−x)=f(x)\), then the function is even. if the resulting function is the opposite of the original function, \(f(−x)=−f(x)\), then the original function is odd. A function as taking things from x, and sending them over to y, where the function f is the map that explains where each element in xis supposed to go. this is visualized in figure 1. For the following exercises, for each pair of functions, find a. \(f g\) b. \(f−g\) c. \(f⋅g\) d. \(f g\). determine the domain of each of these new functions. 1) \(f(x)=3x 4,g(x)=x−2\) 2) \(f(x)=x−8,g(x)=5x^2\).
Comments are closed.