Solved Given A Simple Graph G V E We Define Its Chegg

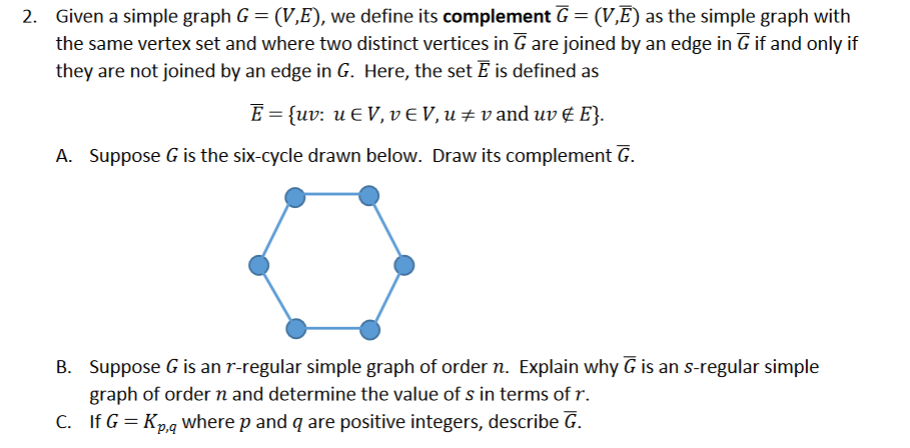
Solved Given A Simple Graph G V E We Define Its Chegg Given a simple graph g = (v, e), we define its complement g ˉ = (v, e ˉ) as the simple graph with the same vertex set and where two distinct vertices in g ˉ are joined by an edge in g ˉ if and only if they are not joined by an edge in g. Let g = (v, e) be a simple undirected graph with n = |v | ≥ 1 vertices. a subset u ⊆ v of the vertices is called a vc set if for every edge {i, j} ∈ e either i ∈ u or j ∈ u (or both). let $u^∗$ be.

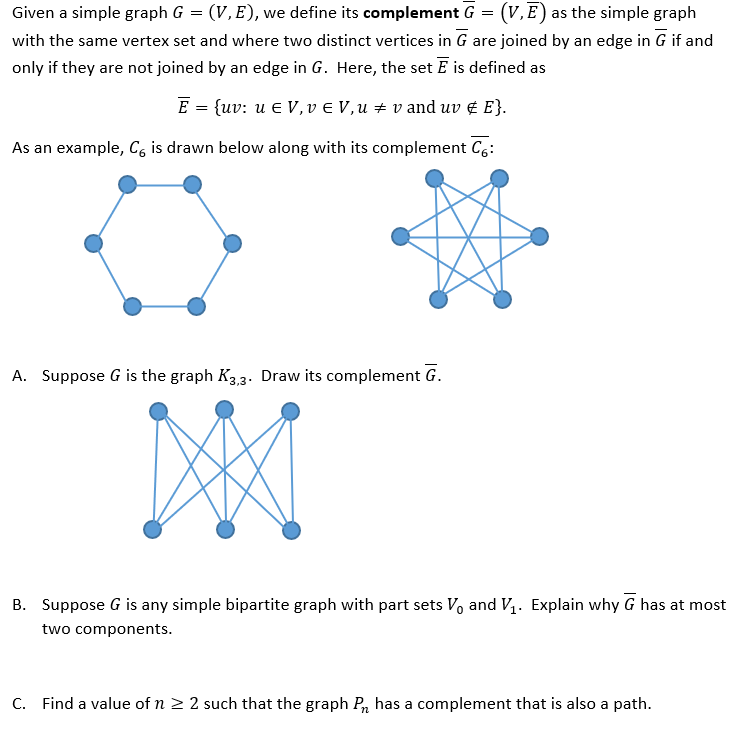
Given A Simple Graph G V E We Define Its Chegg A graph g = (v,e) is bipartite if its vertex set v can be partitioned into two sets l , r (left and right say) such that all edges are between l and r (in other words l and r are independent sets). Let g =(v, e) be a connected, weighted undirected graph whose edges weight may or may not be distinct. given a cut (s, v − s) of s, recall that an edge (u, v) ∈ e is said to cross the cut. There exists a graph on 4 vertices that is isomorphic to its complement by structural analysis, while no graph on 6 vertices can be isomorphic to its complement due to the contradictory nature of edge distributions. Solution: we construct a new graph g′ =(v′;e′) with edge weight w ′∶e′ →r such that v ⊆v , e⊆e ′ and a minimum weight spanning tree of g restricted to gis a maximum weight forest of g.

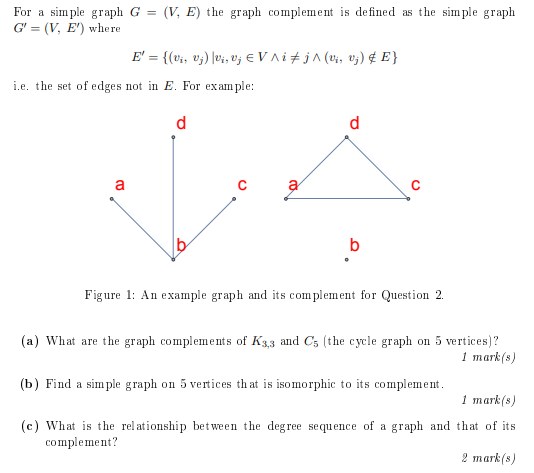
Solved For A Simple Graph G V E The Graph Complement Is Chegg There exists a graph on 4 vertices that is isomorphic to its complement by structural analysis, while no graph on 6 vertices can be isomorphic to its complement due to the contradictory nature of edge distributions. Solution: we construct a new graph g′ =(v′;e′) with edge weight w ′∶e′ →r such that v ⊆v , e⊆e ′ and a minimum weight spanning tree of g restricted to gis a maximum weight forest of g. Show that g has exactly one cycle. let g have n vertices and n edges. since g is a connected g. aph, it has a spanning . in t , with its endpoints u and v. there is a unique path betwee. u and v in t (since t is a tr. e). the union of e and is a cycle. suppo. e that there is some other cycle . if does not contain e, then it is contained in t , . The distance between two vertices u,v in a graph is defined to be the length of the shortest path joining u,v. (in the case the graph is disconnected, this may not be well defined.) 8. let g = (v,e) be a graph. the complement g of g is a graph with the same vertex set as g and e(g) = {e 6∈e(g)}. i.e. g has edges exactly where there are no. We specify a simple graph by its set of vertices and set of edges, treating the edge set as a set of unordered pairs of vertices and write e = uv (or e = vu) for an edge e with endpoints u and v. when u and v are endpoints of an edge, they are adjacent and are neighbors. An independent set uof vertices in g= (v;e) is a set u v of vertices in g so that no pair of vertices in uare adjacent. using the above notation, we then have the following theorem:.

Solved 3 Given A Graph G V E We Define The Graph G Chegg Show that g has exactly one cycle. let g have n vertices and n edges. since g is a connected g. aph, it has a spanning . in t , with its endpoints u and v. there is a unique path betwee. u and v in t (since t is a tr. e). the union of e and is a cycle. suppo. e that there is some other cycle . if does not contain e, then it is contained in t , . The distance between two vertices u,v in a graph is defined to be the length of the shortest path joining u,v. (in the case the graph is disconnected, this may not be well defined.) 8. let g = (v,e) be a graph. the complement g of g is a graph with the same vertex set as g and e(g) = {e 6∈e(g)}. i.e. g has edges exactly where there are no. We specify a simple graph by its set of vertices and set of edges, treating the edge set as a set of unordered pairs of vertices and write e = uv (or e = vu) for an edge e with endpoints u and v. when u and v are endpoints of an edge, they are adjacent and are neighbors. An independent set uof vertices in g= (v;e) is a set u v of vertices in g so that no pair of vertices in uare adjacent. using the above notation, we then have the following theorem:.