Solved In A Logistic Growth Population Model The Value K Chegg

Solved In A Logistic Growth Population Model The Value K Chegg # logistic growth population model in a logistic growth population model, the population dynamics a. Describe the concept of environmental carrying capacity in the logistic model of population growth. draw a direction field for a logistic equation and interpret the solution curves. solve a logistic equation and interpret the results.

Solved The Logistic Equation Models The Growth Of A Chegg Study with quizlet and memorize flashcards containing terms like logistic growth , carrying capacity , rmax and more. The logistic growth model is clearly a separable differential equation, but separating variables leaves you with an integral that requires integration using partial fractions decomposition and then still requires a messy amount of algebra. To this model, when p reaches k, the growth rate is 0, and the population will be stable. if p were to somehow exceed k, the rate would become negative and the population would decrease toward k. in order to solve equation 5.2, we separate the variables first and integrate both sides: z dp p = 1− p k z kdp (k − ) z rdt. Consider the logistic differential equation subject to an initial population of p 0 p 0 with carrying capacity k k and growth rate r r. the solution to the corresponding initial value problem is given by. p (t)= p 0kert (k−p 0) p 0ert p (t) = p 0 k e r t (k p 0) p 0 e r t.

Solved A The Logistic Model Of Population Growth Uses The Chegg To this model, when p reaches k, the growth rate is 0, and the population will be stable. if p were to somehow exceed k, the rate would become negative and the population would decrease toward k. in order to solve equation 5.2, we separate the variables first and integrate both sides: z dp p = 1− p k z kdp (k − ) z rdt. Consider the logistic differential equation subject to an initial population of p 0 p 0 with carrying capacity k k and growth rate r r. the solution to the corresponding initial value problem is given by. p (t)= p 0kert (k−p 0) p 0ert p (t) = p 0 k e r t (k p 0) p 0 e r t. Our expert help has broken down your problem into an easy to learn solution you can count on. question: 3) a logistic growth model can be used model population growth when there are limited resources to support the population. More realistic models for population growth take environmental factors into account: every population has a carrying capacity based on the population’s survival needs and the environment they inhabit. By assuming that the per capita growth rate decreases as the population grows, we are led to the logistic model of population growth, which predicts that the population will eventually stabilize at the carrying capacity. Using this, we have the logistic population model. dp = ⎛ kp ⎜ 1 − p ⎞ ⎟ dt ⎝ k ⎠ this differential equation can be solved using separation of variables, where partial fractions are used in the integration process (see pp. 538 539 of stewart textbook). doing this gives the solution .
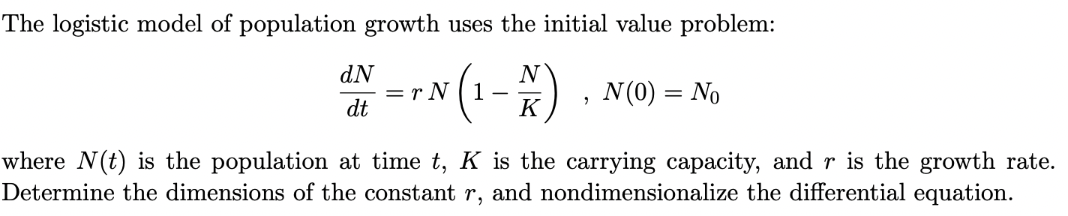
Solved The Logistic Model Of Population Growth Uses The Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: 3) a logistic growth model can be used model population growth when there are limited resources to support the population. More realistic models for population growth take environmental factors into account: every population has a carrying capacity based on the population’s survival needs and the environment they inhabit. By assuming that the per capita growth rate decreases as the population grows, we are led to the logistic model of population growth, which predicts that the population will eventually stabilize at the carrying capacity. Using this, we have the logistic population model. dp = ⎛ kp ⎜ 1 − p ⎞ ⎟ dt ⎝ k ⎠ this differential equation can be solved using separation of variables, where partial fractions are used in the integration process (see pp. 538 539 of stewart textbook). doing this gives the solution .
Comments are closed.