Solved Two Operators D1 I And D2 I Are Said To Commute If Chegg

Solved Two Operators D1 ï And D2 ï Are Said To Commute If Chegg There are 2 steps to solve this one. to prove that [q a, q b] f = Θ, we will start b not the question you’re looking for? post any question and get expert help quickly. (a) it is possible to specify a common eigenbasis of two operators if they commute. if one of the operators is non degenerate, then all of its eigenvectors are also eigenvectors of the other operator.

Solved Two Operators D1 And D2 Are Said To Commute If Their Chegg If two operators commute then both quantities can be measured at the same time, if not then there is a tradeoff in the accuracy in the measurement for one quantity vs. the other. operators are commonly used to perform a specific mathematical operation on another function. We have just seen that the momentum operator commutes with the hamiltonian of a free particle. then the two operators should share common eigenfunctions. this is indeed the case, as we can verify. consider the eigenfunctions for the momentum operator:. For example, the commutator of the operators x^ x ^ and d dx d d x, denoted by [x^, d dx] [x ^, d d x], is by definition x^ d dx − d dxx^ x ^ d d x d d x x ^. when [a^,b^] = 0 [a ^, b ^] = 0, the operators a^ a ^ and b^ b ^ are said to commute. therefore, if the operators a^ a ^ and b^ b ^ commute, then a^b^ = b^a^ a ^ b ^ = b ^ a ^. Commutative operators: two operators are said to be commutative if the following relation is true: [Â, Ê ] = [ Â Ê Ê Â ] = 0 , where a and e are two operators.

Solved 1 Show That The Operators 1 And I Do Not Commute Chegg For example, the commutator of the operators x^ x ^ and d dx d d x, denoted by [x^, d dx] [x ^, d d x], is by definition x^ d dx − d dxx^ x ^ d d x d d x x ^. when [a^,b^] = 0 [a ^, b ^] = 0, the operators a^ a ^ and b^ b ^ are said to commute. therefore, if the operators a^ a ^ and b^ b ^ commute, then a^b^ = b^a^ a ^ b ^ = b ^ a ^. Commutative operators: two operators are said to be commutative if the following relation is true: [Â, Ê ] = [ Â Ê Ê Â ] = 0 , where a and e are two operators. Determine whether or not the following pairs of operators commute. b^a^ (b) x dxd (c) sqr sqrt (d) x2dxddx2d2. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: determine whether or not the following pairs of operators commute. In quantum mechanics two observables a and b of a quantum system can be predicted (found) exactly only if the outcomes of the measurements of the two observables are independent. Hermitian operators are an exception; so are anti hermitian and unitary operators. we de ne an operator to be normal if it commutes with its hermitian conjugate, [a;a y ] = 0. Two operators commute if the following equation is true: [a^,e^] = a^e^ −e^a^ = 0 (4.6.2) (4.6.2) [a ^, e ^] = a ^ e ^ e ^ a ^ = 0. to determine whether two operators commute first operate a^e^ a ^ e ^ on a function f(x) f (x). then operate e^a^ e ^ a ^ the same function f(x) f (x).
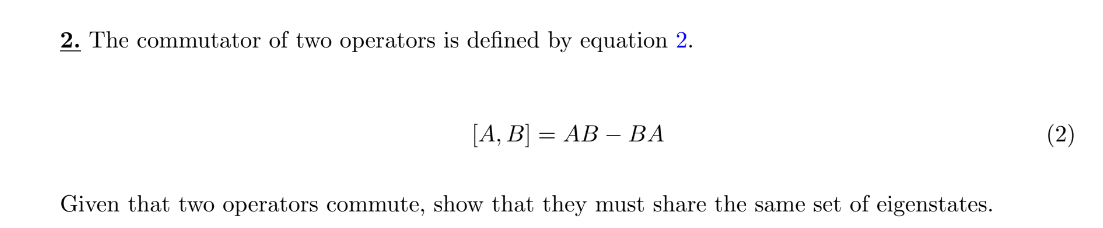
Solved 2 The Commutator Of Two Operators Is Defined By Chegg Determine whether or not the following pairs of operators commute. b^a^ (b) x dxd (c) sqr sqrt (d) x2dxddx2d2. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: determine whether or not the following pairs of operators commute. In quantum mechanics two observables a and b of a quantum system can be predicted (found) exactly only if the outcomes of the measurements of the two observables are independent. Hermitian operators are an exception; so are anti hermitian and unitary operators. we de ne an operator to be normal if it commutes with its hermitian conjugate, [a;a y ] = 0. Two operators commute if the following equation is true: [a^,e^] = a^e^ −e^a^ = 0 (4.6.2) (4.6.2) [a ^, e ^] = a ^ e ^ e ^ a ^ = 0. to determine whether two operators commute first operate a^e^ a ^ e ^ on a function f(x) f (x). then operate e^a^ e ^ a ^ the same function f(x) f (x).

Solved Problem 1 Given The Operators â X And ê D Dx Chegg Hermitian operators are an exception; so are anti hermitian and unitary operators. we de ne an operator to be normal if it commutes with its hermitian conjugate, [a;a y ] = 0. Two operators commute if the following equation is true: [a^,e^] = a^e^ −e^a^ = 0 (4.6.2) (4.6.2) [a ^, e ^] = a ^ e ^ e ^ a ^ = 0. to determine whether two operators commute first operate a^e^ a ^ e ^ on a function f(x) f (x). then operate e^a^ e ^ a ^ the same function f(x) f (x).

Solved Problem 1 Given The Operators â X And ê D Dx Chegg
Comments are closed.