Solved Using Laplace Domain S Domain Analysis Determine Chegg

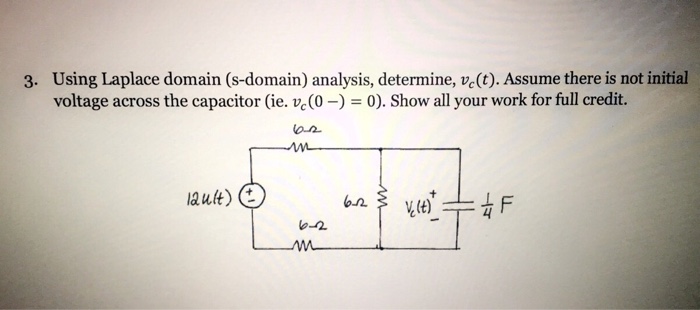
Solved Using Laplace Domain S Domain Analysis Determine Chegg Question: name: eee202 week 13 lesson 3 circuit analysis using laplace transform assignment problem 1 (30 points): for circuit elements shown in the time domain using the s domain representation, determine the source current in the s domain and time domain: where: r=4Ωl=50mh:il(0)=0c=200μf:vc(0)=0vs(t)=4(1−e−250t)v. We merely need to transform a complicated set of mathematical relationships in the time domain into the s domain where we convert operators (derivatives and integrals) into simple multipliers of s and 1 s. this now allows us to use algebra to set up and solve our circuit equations.

Solved 1 Using S Domain Analysis Laplace Transform Chegg Using the laplace transform to solve a second order circuit. the method requires that the circuit be converted from the time domain to the s domain and then solved for v(s). Find out how to transform time domain circuit elements (resistors, capacitors, inductors) into the s domain using laplace transforms. develop the ability to solve linear time invariant (lti) circuits using the s domain techniques, including nodal and mesh analysis. It converts the time domain circuit to the frequency domain for easy analysis. to solve the circuit using laplace transform, we follow the following steps: write the differential equation of the given circuit. take the laplace transform of the equation written. analysis of the s domain equations. Note the source transformation rules apply! switch in place since t= ∞, closed at t=0. solve for vc(t). $% = eq ! % $ sl ! the switch has been open for a long time and is closed at t=0.

Class Exercise Laplace Domain Analysis Pdf It converts the time domain circuit to the frequency domain for easy analysis. to solve the circuit using laplace transform, we follow the following steps: write the differential equation of the given circuit. take the laplace transform of the equation written. analysis of the s domain equations. Note the source transformation rules apply! switch in place since t= ∞, closed at t=0. solve for vc(t). $% = eq ! % $ sl ! the switch has been open for a long time and is closed at t=0. First we need to determine the s domain circuit that best fits our need: (series equivalent for current) summing the voltages around the mesh: repeating the problem by solving for v: the s domain circuit that best fits our need is a parallel equivalent for voltage. Circuit analysis via laplace transform 7{14 † theforcedresponseislinearinu(s),i.e.,theindependentsourcesignals † thenaturalresponseislinearinw,i.e.,theinductor&capacitorinitial. Resistors in the laplace domain ohm’s law governs the behavior of resistors. 𝑣𝑣𝑡𝑡= 𝑅𝑅⋅𝑖𝑖𝑡𝑡or 𝑖𝑖𝑡𝑡= 1 𝑅𝑅. 𝑣𝑣𝑡𝑡 laplace transforming these expressions gives us ohm’s law in the laplace domain: 𝑉𝑉𝑠𝑠= 𝑅𝑅⋅𝐼𝐼𝑠𝑠or 𝐼𝐼𝑠𝑠= 1 𝑅𝑅. Demonstrates the utility of symbolic algebra by using the laplace transform to solve a second order circuit. the method requires that the circuit be converted from the time domain to the s domain and then solved for v(s).

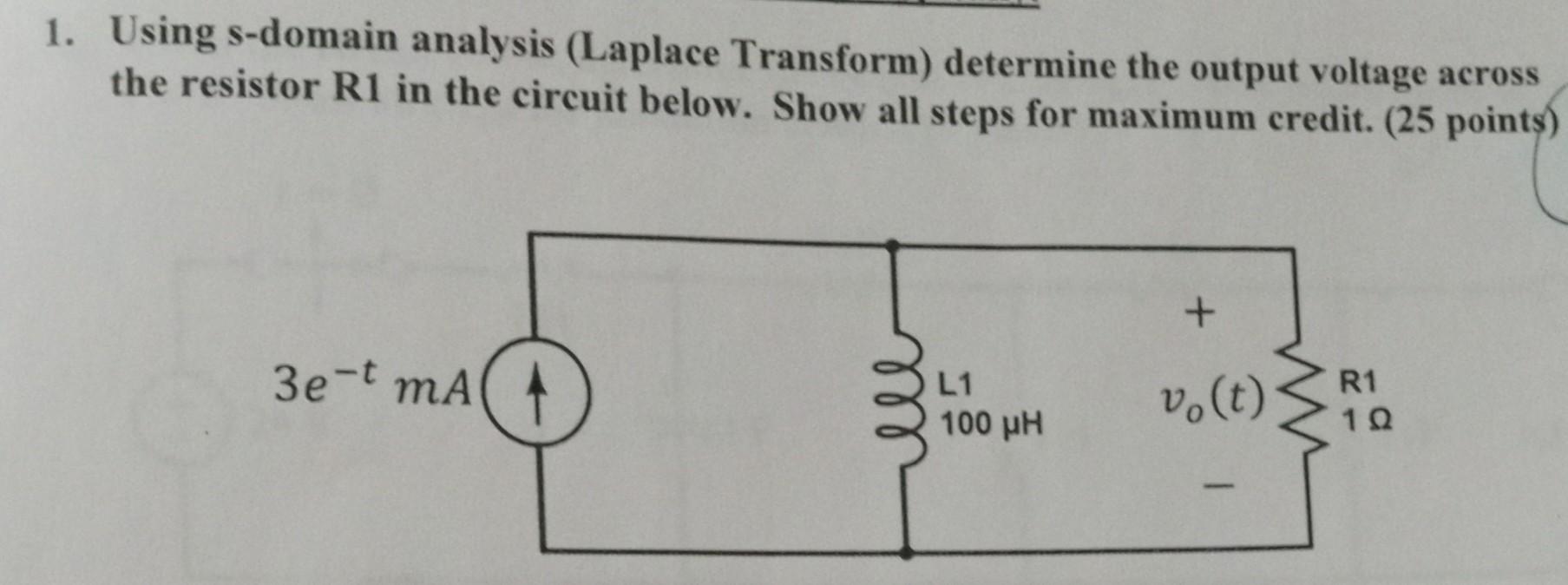
Solved Using The Laplace Domain Determine The System S Chegg First we need to determine the s domain circuit that best fits our need: (series equivalent for current) summing the voltages around the mesh: repeating the problem by solving for v: the s domain circuit that best fits our need is a parallel equivalent for voltage. Circuit analysis via laplace transform 7{14 † theforcedresponseislinearinu(s),i.e.,theindependentsourcesignals † thenaturalresponseislinearinw,i.e.,theinductor&capacitorinitial. Resistors in the laplace domain ohm’s law governs the behavior of resistors. 𝑣𝑣𝑡𝑡= 𝑅𝑅⋅𝑖𝑖𝑡𝑡or 𝑖𝑖𝑡𝑡= 1 𝑅𝑅. 𝑣𝑣𝑡𝑡 laplace transforming these expressions gives us ohm’s law in the laplace domain: 𝑉𝑉𝑠𝑠= 𝑅𝑅⋅𝐼𝐼𝑠𝑠or 𝐼𝐼𝑠𝑠= 1 𝑅𝑅. Demonstrates the utility of symbolic algebra by using the laplace transform to solve a second order circuit. the method requires that the circuit be converted from the time domain to the s domain and then solved for v(s).