Solving Exponential Equations Using Common Logarithms Or Natural Logarithms

How To Solve An Exponential Equation By Using Natural Logarithms Worksheets Library 1) keep the exponential expression by itself on one side of the equation. 2) get the logarithms of both sides of the equation. you can use any bases for logs. 3) solve for the variable. keep the answer exact or give decimal approximations. When an exponential equation cannot be rewritten with a common base, solve by taking the logarithm of each side. we can solve exponential equations with base \(e\), by applying the natural logarithm of both sides and then using the fact that \( \ln (e^u) = u \).
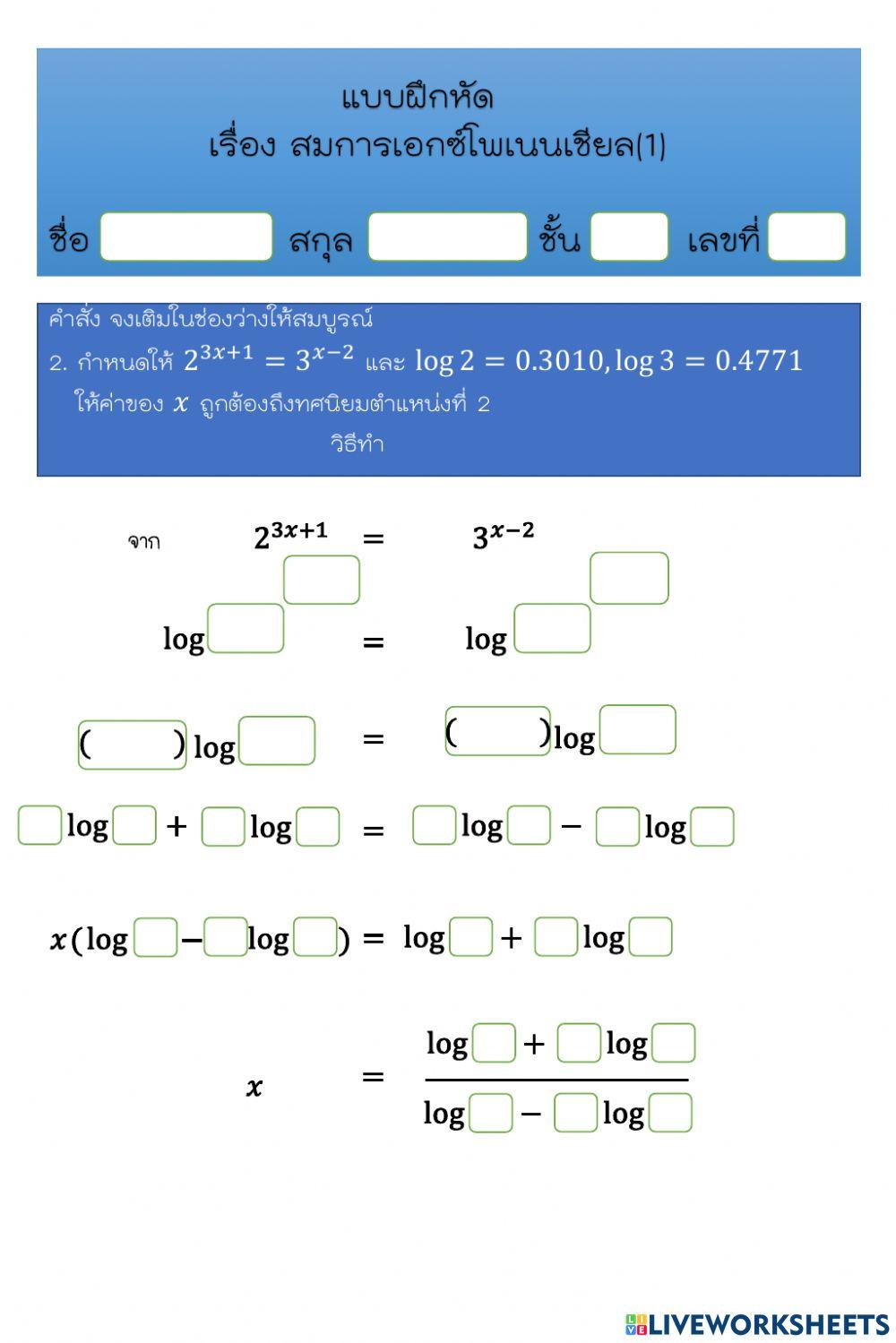
Solving Exponential Equations Using Logarithms Worksheets 1 Worksheets Library In solving these more complicated equations, you will have to use logarithms. taking logarithms will allow us to take advantage of the log rule that says that powers inside a log can be moved out in front as multipliers. Sometimes, we need to use properties of logarithms to solve equations. example: solve log. 4. x – 3 log. 4. 2 = log. 4. 5. log. 𝑏𝑏. 𝑚𝑚. 𝑝𝑝 = 𝑝𝑝log. 𝑏𝑏. 𝑚𝑚. How to: given an exponential equation in which a common base cannot be found, solve for the unknown. apply the logarithm of both sides of the equation. if one of the terms in the equation has base 10, use the common logarithm. if none of the terms in the equation has base 10, use the natural logarithm. use the rules of logarithms to solve for. Use the method of common bases to solve exponential equations. use logarithms to solve exponential equations. use the definition of a logarithm to solve logarithmic equations. use the one to one property of logarithms to solve logarithmic equations. if bx = by then x = y.

How To Solve An Advanced Exponential Equation By Using Natural Worksheets Library How to: given an exponential equation in which a common base cannot be found, solve for the unknown. apply the logarithm of both sides of the equation. if one of the terms in the equation has base 10, use the common logarithm. if none of the terms in the equation has base 10, use the natural logarithm. use the rules of logarithms to solve for. Use the method of common bases to solve exponential equations. use logarithms to solve exponential equations. use the definition of a logarithm to solve logarithmic equations. use the one to one property of logarithms to solve logarithmic equations. if bx = by then x = y. Solve each equation. if an exponential equation, express the solution set in terms of natural logarithms or common logarithms. use a calculator to find the decimal approximation for the solution, rounding to two decimal places. 1.3x = 21[x = ln21 ln3 ≈2.77] 2.5e2x = 20[x = ln4 2 ≈0.69] 3. log 5(3x−4) = 3[x = 43] 4.2ln(4x) = 10[x = e5 4. When solving exponential equations using logarithms, we often apply two important properties of logarithms: the power property of logs and the change of base property of logs: we most often use the change of base property when we wish to use our calculators to evaluate logs. Solve exponential equations using logarithms. in the following exercises, solve each exponential equation. find the exact answer and then approximate it to three decimal places. Apply the logarithm of both sides of the equation. if one of the terms in the equation has base 10, use the common logarithm. if none of the terms in the equation has base 10, use the natural logarithm. use the rules of logarithms to solve for the unknown. solve 5x 2 = 4x 5 x 2 = 4 x. solution.
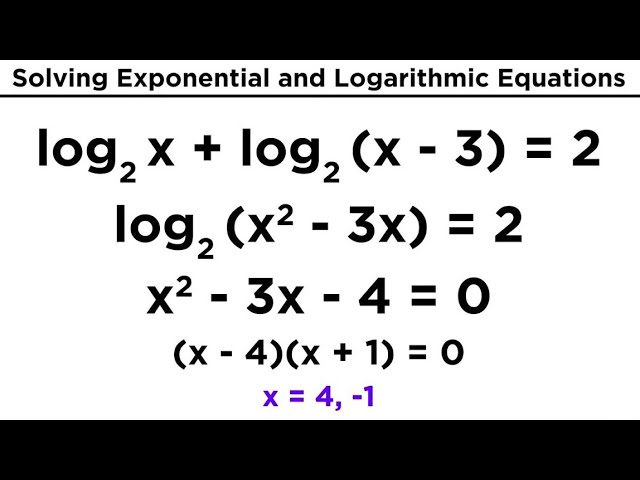
Properties Of Logarithms Activities Solving Exponential Worksheets Library Solve each equation. if an exponential equation, express the solution set in terms of natural logarithms or common logarithms. use a calculator to find the decimal approximation for the solution, rounding to two decimal places. 1.3x = 21[x = ln21 ln3 ≈2.77] 2.5e2x = 20[x = ln4 2 ≈0.69] 3. log 5(3x−4) = 3[x = 43] 4.2ln(4x) = 10[x = e5 4. When solving exponential equations using logarithms, we often apply two important properties of logarithms: the power property of logs and the change of base property of logs: we most often use the change of base property when we wish to use our calculators to evaluate logs. Solve exponential equations using logarithms. in the following exercises, solve each exponential equation. find the exact answer and then approximate it to three decimal places. Apply the logarithm of both sides of the equation. if one of the terms in the equation has base 10, use the common logarithm. if none of the terms in the equation has base 10, use the natural logarithm. use the rules of logarithms to solve for the unknown. solve 5x 2 = 4x 5 x 2 = 4 x. solution.
Comments are closed.