Tn 11th English Half Yearly Question Paper 2024 Pdf Aglasem

Tn 11th English Half Yearly Question Paper 2024 Pdf Aglasem Okay so when my professor was going over it in class it seemed quite simple, but when i got to my homework i became confused. this is a homework example. for (int i = 0; i < n; i ) i kno. I believe you are right. the recurrence relation will always split into two parts, namely t (n 1) and t (n 2). looking at these two, it is clear that n 1 decreases in value slower than n 2, or in other words, you will have more branches from the n 1 portion of the tree. despite this, when considering big o, it is useful to just consider the 'worst case' scenario, which in this case is that.

Tn 11th Maths Half Yearly Question Paper 2023 Pdf 2 the comment from johnny mopp is pretty cool (though i think the order should be ['tn', 'fn', 'fp', 'tp'], but if i came across it in code i'd have to think twice. (i can count on one hand the number of times i've seen bit shift operations in production code.) there's a new way to handle things like this in python 3.10: structural pattern. From article on o notation: "a function t (n) that will express how long the algorithm will take to run (in some arbitrary measurement of time) in terms of the number of elements in the input set.". I have the following worked out: t(n) = t(n 1) n = o(n^2) now when i work this out i find that the bound is very loose. have i done something wrong or is it just that way?. Can i extract tp,tn,fp and fn as numbers from confusion matrix with pycaret or they are only given as plot?.

Tamil Nadu 11th Question Paper 2022 For English Pdf I have the following worked out: t(n) = t(n 1) n = o(n^2) now when i work this out i find that the bound is very loose. have i done something wrong or is it just that way?. Can i extract tp,tn,fp and fn as numbers from confusion matrix with pycaret or they are only given as plot?. How to solve the recurrence relation t(n) = 8t(n 2) 100 n^2 by the master's theorem. Can anybody please explain the time complexity of t(n)=2t(n 4) o(1) using recurrence tree? i saw somewhere it says o(n^1 2). From calculating the first numbers you can quickly suspect that the solution is t(n) = n. you can then prove this using mathematical induction: basis: for the first element, n = 4, we can calculate the value like: t(4) = t(3) t(1) t(0) = 3 1 0 = 4 so the statement is true. inductive step: assuming t(n) = n, show that t(n 1) = n 1: t(n 1) = t(n) t(n 2) t(n 3) = n (n 2) (n 3. Can someone please help me with this ? use substitution method to solve it. t(n) = t(n 1) n^4 explanation of steps would be greatly appreciated.

Tn 11th English Public Question Paper 2024 Pdf Download Tamil Nadu Board Pyqp Aglasem How to solve the recurrence relation t(n) = 8t(n 2) 100 n^2 by the master's theorem. Can anybody please explain the time complexity of t(n)=2t(n 4) o(1) using recurrence tree? i saw somewhere it says o(n^1 2). From calculating the first numbers you can quickly suspect that the solution is t(n) = n. you can then prove this using mathematical induction: basis: for the first element, n = 4, we can calculate the value like: t(4) = t(3) t(1) t(0) = 3 1 0 = 4 so the statement is true. inductive step: assuming t(n) = n, show that t(n 1) = n 1: t(n 1) = t(n) t(n 2) t(n 3) = n (n 2) (n 3. Can someone please help me with this ? use substitution method to solve it. t(n) = t(n 1) n^4 explanation of steps would be greatly appreciated.

Tn 11th English Half Yearly Question Paper 2024 Pdf Aglasem From calculating the first numbers you can quickly suspect that the solution is t(n) = n. you can then prove this using mathematical induction: basis: for the first element, n = 4, we can calculate the value like: t(4) = t(3) t(1) t(0) = 3 1 0 = 4 so the statement is true. inductive step: assuming t(n) = n, show that t(n 1) = n 1: t(n 1) = t(n) t(n 2) t(n 3) = n (n 2) (n 3. Can someone please help me with this ? use substitution method to solve it. t(n) = t(n 1) n^4 explanation of steps would be greatly appreciated.
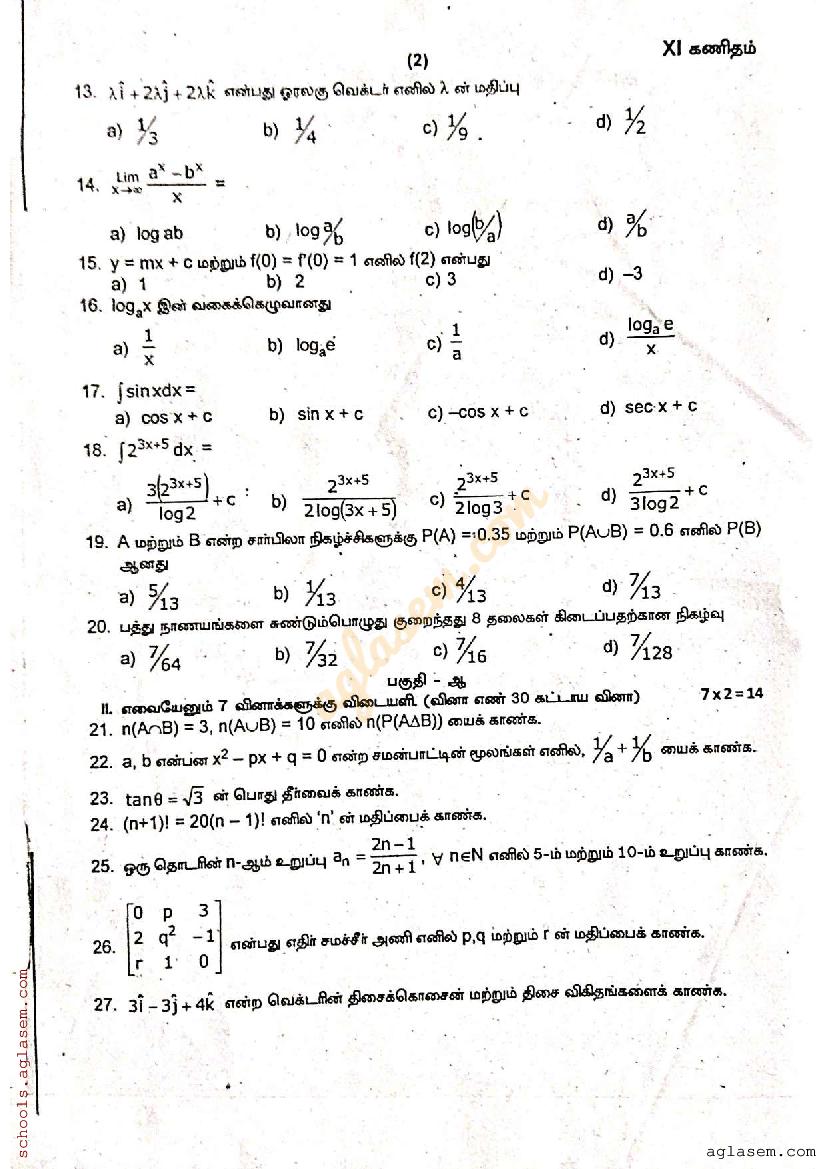
Tn 11th Maths Half Yearly Question Paper 2023 Pdf
Comments are closed.