Travelling Salesman Problem Pdf Integer Computer Science Programming Paradigms This section explores hamilton paths and circuits, their significance in graph theory, and their application in optimizing routes like school buses in boston, saving $5 million annually. Explore the traveling salesman problem, hamilton circuits, and algorithms like brute force and nearest neighbor. learn to solve tsps with weighted graphs.
Hamiltonian Circuits The Traveling Salesman Problem Pdf Mathematical Concepts Combinatorics In this section, we will analyze hamilton cycles in complete weighted graphs to find the shortest route to visit a number of locations and return to the starting point. In the theory of computational complexity, the travelling salesman problem (tsp) asks the following question: "given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?". Suppose you want to use the brute force algorithm to solve the tsp for a graph with 12 vertices, that you can compute the weight of one hamilton circuit in 10 minutes and that the fate of the world rests on your results. Finding a shortest hamiltonian circuit on a weighted graph is called the traveling salesman problem (tsp) because the question can be framed like this: suppose a salesman needs to give sales pitches in four cities. he looks up the airfares between each city, and puts the costs in a graph.
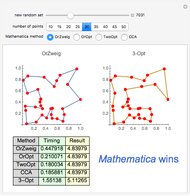
Traveling Salesman Problem Wolfram Demonstrations Project Suppose you want to use the brute force algorithm to solve the tsp for a graph with 12 vertices, that you can compute the weight of one hamilton circuit in 10 minutes and that the fate of the world rests on your results. Finding a shortest hamiltonian circuit on a weighted graph is called the traveling salesman problem (tsp) because the question can be framed like this: suppose a salesman needs to give sales pitches in four cities. he looks up the airfares between each city, and puts the costs in a graph. In this section we will talk about hamiltonian circuits, hamiltonian paths, the travelling salesman problem, a few famous graph theory algorithms, and more! remember the difference between a circuit and a path? a circuit is a special type of path that starts and ends at the same vertex. Pick a reference vertex to start at, and use the nearest neighbor algorithm to nd a hamilton circuit. Our problem is to visit all of the locations exactly once, that is, to find a hamilton circuit—there are many of these—we want to find the best one! “best” might mean “fastest”, “shortest”, “cheapest” or something else. look at the book’s examples 4, 5 and 6. The petersen graph icosahedron examples of graphs: do they have a hamilton circuit? the only reason a connected graph has no euler circuit is that it has odd vertices. but there is no "nice" reason that explains when a graph has no hamilton circuit. 3. if the graph has an edge that is a bridge.
Comments are closed.