What Are The Types Of Numbers Real Vs Imaginary Rational Irrational Zero Math

What Are The Types Of Numbers Real Vs Imaginary Rational Vs Irrational Youtube What are the types of numbers | natural numbers | whole numbers | integers | real numbers | imaginary number | zero mathabout video :hello all, in this video. Real numbers (): numbers that correspond to points along a line. they can be positive, negative, or zero. all rational numbers are real, but the converse is not true. irrational numbers (): real numbers that are not rational.

Rational Vs Irrational Numbers What Is The Main Difference 7esl Types of numbers in mathematics include various types of numbers i.e., natural numbers, whole numbers, integers, rational numbers, irrational numbers, real numbers, imaginary numbers, complex numbers, prime numbers, composite numbers, even numbers, odd numbers etc. From natural numbers to real numbers to the imaginary numbers of quaternions, the concepts learned in number systems can be challenging for students to remember and use practically. The content outlines the classifications of numbers in mathematics, distinguishing between real numbers and imaginary (complex) numbers. real numbers include rational and irrational numbers, while imaginary numbers are derived to solve equations lacking real solutions. The classifications of numbers are: real, imaginary, whole, rational and irrational, natural and negative, even and odd, and fractions. learn more about numbers!.
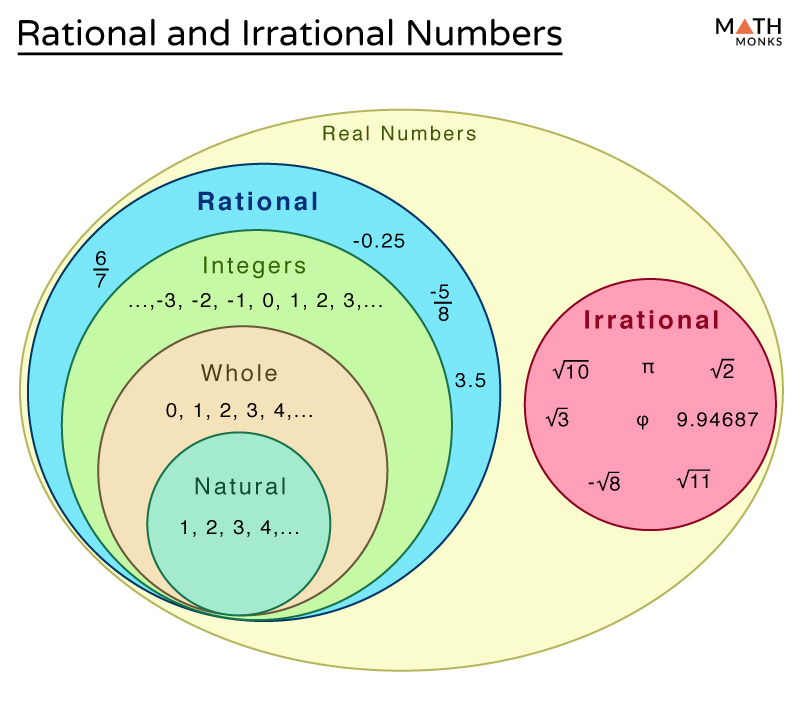
Rational And Irrational Numbers Differences Examples The content outlines the classifications of numbers in mathematics, distinguishing between real numbers and imaginary (complex) numbers. real numbers include rational and irrational numbers, while imaginary numbers are derived to solve equations lacking real solutions. The classifications of numbers are: real, imaginary, whole, rational and irrational, natural and negative, even and odd, and fractions. learn more about numbers!. It turns out that most other roots are also irrational. the constants π and e are also irrational. just like rational numbers have repeating decimal expansions (or finite ones), the irrational numbers have no repeating pattern. together, the irrational and rational numbers are called the real numbers which are often written as . these are all. Combinations of real and imaginary numbers make up the complex numbers. here are some algebraic equations, and the number set needed to solve them: we can take an existing set symbol and place in the top right corner: set of positive integers {1, 2, 3, } set of nonzero integers { , 3, 2, 1, 1, 2, 3, }. It can be natural numbers, whole numbers, integers, rational numbers, and irrational numbers. irrational numbers are real numbers, but not all real numbers are irrational numbers. a real number is denoted by the letter ‘r.’. Historically, first occurred the set of natural numbers; rather quickly expanded with fractions, and even with positive irrational numbers; zero and negative numbers were discovered only after these subsets of real numbers.

Rational Vs Irrational Real Numbers By Foiled By Math Tpt It turns out that most other roots are also irrational. the constants π and e are also irrational. just like rational numbers have repeating decimal expansions (or finite ones), the irrational numbers have no repeating pattern. together, the irrational and rational numbers are called the real numbers which are often written as . these are all. Combinations of real and imaginary numbers make up the complex numbers. here are some algebraic equations, and the number set needed to solve them: we can take an existing set symbol and place in the top right corner: set of positive integers {1, 2, 3, } set of nonzero integers { , 3, 2, 1, 1, 2, 3, }. It can be natural numbers, whole numbers, integers, rational numbers, and irrational numbers. irrational numbers are real numbers, but not all real numbers are irrational numbers. a real number is denoted by the letter ‘r.’. Historically, first occurred the set of natural numbers; rather quickly expanded with fractions, and even with positive irrational numbers; zero and negative numbers were discovered only after these subsets of real numbers.
Comments are closed.